Gen0012(08)boxplotで能力値検討 [確率統計]
MAクラスの能力値(Tt)の分布の世代変化を箱ひげ図(Box-whisker plot)にして観察する。
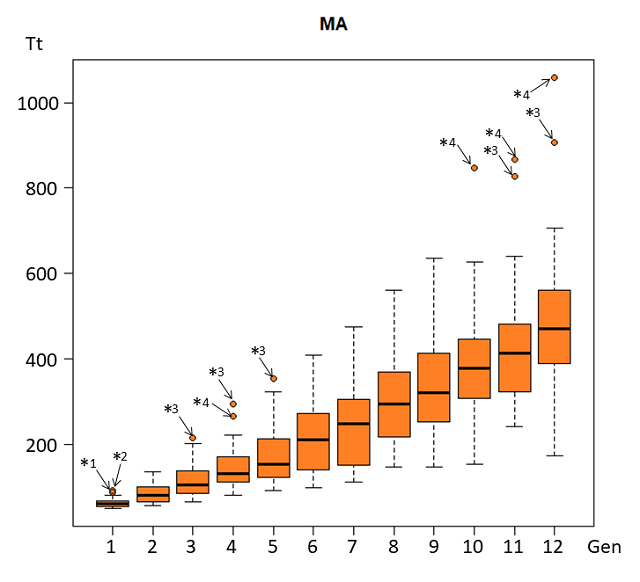
注)*1)平忠正、*2)平経俊、*3)源範頼、*4)平長盛
箱ひげ図(Box-whisker plot)の見方をみると箱の中に引いてある横線は中央値であり、平均値ではない。なるほど、平均値は箱の中心になるのでわざわざ表示する必要はない。中央値ならば、それが中央からずれていれば分布の形が左右対称ではないということが分かる。第3世代(Gen0003)~第5世代(Gen0005)の中央値が下側にあるということは、Tt値が大きい一部のメンバーが平均値を押し上げているということで分布の形がTt値の大きい方に尾を引いているということが分かる。
箱はデータがTtの値が小さい順に並べ4等分したとき、下から4分の1~4分の3の順位のメンバーが入っている値の範囲を示している。
箱から上下に引かれた破線の頂点にある横線は、最小値と最大値を示すが、それは下側境界点と上側境界点の内部にあるデータに限られる。それを外れた値は外れ値となり丸で示す。
下側境界点と上側境界点は箱の高さ(全データの中間的な50%が入るデータの範囲)の1.5倍箱から離れた点である。
MAのグラフを見ると、世代ごとに能力値は高くなる(成長している)。能力値のばらつきが大きくなっている。
外れ値を観察すると外れ値は上側にあり、他より能力がかなり高いメンバーがいるということを示している。ならば、優勝してもいいようなものだが、
第1世代(Gen0001)では、https://ykdn.blog.ss-blog.jp/2019-09-16 源為宗(優勝)、源範頼(優勝同点)、平忠清(優勝同点)だった。 *1の平忠正は7勝8敗と負け越し、*2の平経俊は9勝6敗であった。
第3世代(Gen0003)では https://ykdn.blog.ss-blog.jp/2019-09-16 源為宗(優勝)、源範頼(優勝同点)、平忠清(優勝同点)であり、*3の源範頼は外れ値にふさわしい成績であった。
第4世代(Gen0004) https://ykdn.blog.ss-blog.jp/2019-09-28 では、源為朝が優勝しており、*3の源範頼は9勝6敗、*4の平長盛も9勝6敗と外れ値のメンバーとしては期待外れの成績であった。
第5世代(Gen0005)https://ykdn.blog.ss-blog.jp/2019-10-12 では、平忠盛(優勝)、平正綱(優勝同点)であり、*3の源範頼は5勝10敗と大きく負け越した。
以上能力どおりの成績とはなったおらず、「勝負は時の運」、「勝負は水物」というにふさわしいものとなっている。つまりは、現実でもこのような偶然の力によるものがあってもいいことを意味している。
第10世代(Gen0010)https://ykdn.blog.ss-blog.jp/2019-12-05 では、*4の平長盛は6勝9敗であり、https://ykdn.blog.ss-blog.jp/2019-12-06 「対戦前の実力(能力パラメータ)値による平長盛の平均勝率は0.683126(10.2勝 4.8敗)。乱数による偶然の力が現れている。」としている。
第11世代(Gen0011)https://ykdn.blog.ss-blog.jp/2019-12-13でやっと*4の平長盛が優勝した。でも、今までの結果を踏まえると実力があったから優勝したのか、偶然の力により優勝したのか成績からは区別できない。成績から能力を評価することの難しさをこのシミュレーションは示していると思う。なお、*3の源範頼は11勝4敗の成績であった。
第12世代(Gen0012)https://ykdn.blog.ss-blog.jp/2019-12-20 では、*4の平長盛、*3の源範頼ともに11勝4敗の成績で、優勝は源為朝であった。
以上、外れ値となるような優れた能力であっても優勝できたのは11回中1回のみで優勝同点も11回中1回と能力と成績には強い関連はなかった。
次に上下のクラスとメンバーが入れ替わるJ1について検討する。
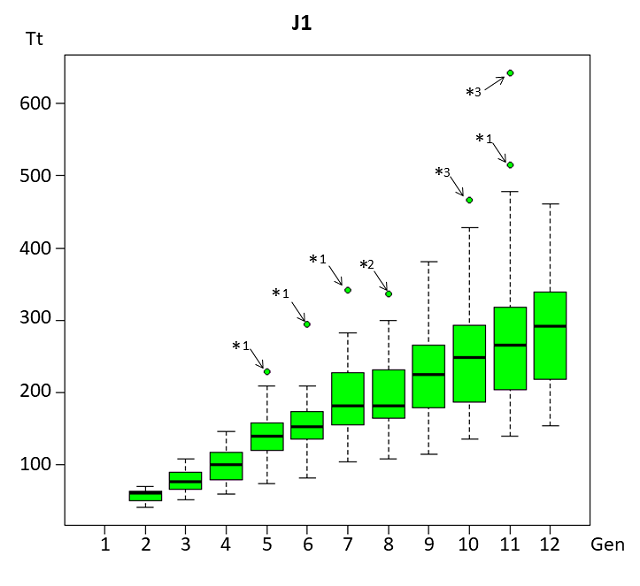
注)*1)平重義、*2)平直材、*3)源満末
第5世代(Gen0005) https://ykdn.blog.ss-blog.jp/2019-10-16 の*1の平重義は前世代J2で14勝1敗の成績で優勝し、ここでは10勝5敗であった。
第6世代(Gen0006) https://ykdn.blog.ss-blog.jp/2019-10-27 の*1の平重義は8勝7敗とやっと勝ち越しの成績であった。
第7世代(Gen0007) https://ykdn.blog.ss-blog.jp/2019-11-09 で*1の平重義がやっと優勝して次世代はMAに昇格する。
第8世代(Gen0008)https://ykdn.blog.ss-blog.jp/2019-11-18 は外れ値は*2の平直材であったが、8勝7敗と平凡な成績であった。
第10世代(Gen0010) https://ykdn.blog.ss-blog.jp/2019-12-06 では*3の源満末がJ1から昇格して優勝した。
第11世代(Gen0011)https://ykdn.blog.ss-blog.jp/2019-12-14 では、*3の源満末が大きく離れた値だったが優勝はできなかった。次世代はMAに昇格するのでJ1での外れ値には登場しない。*1の平重義はMAから降格して今世代で優勝し次世代はMAに再昇格する。
J1は成績優秀者がMAに昇格することで外れ値が消える傾向にある。
*1の平重義が良い成績をなかなか上げられずMAに昇格できなく3世代連続して外れ値として登場し、またMAから陥落することによりJ1では能力が外れ値となり11回中4回も登場した。
MAとJ1のグラフを重ねて比較する。
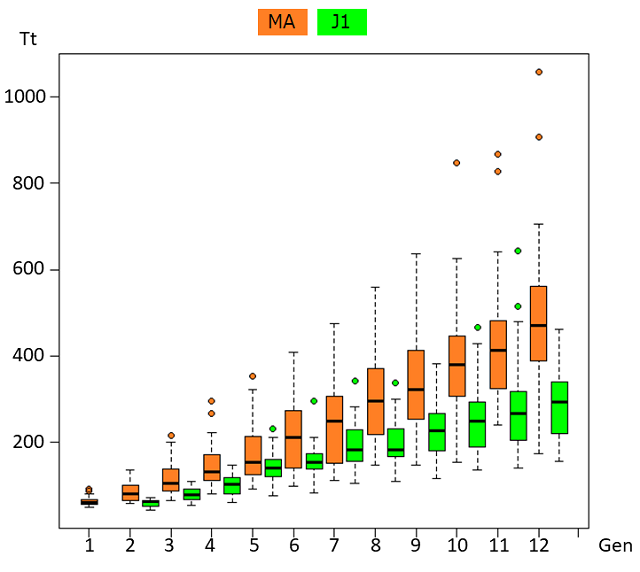
M1とJ1との差が徐々に開いてきた。能力が低くMAから降格するべき者は既に降格してしまっていると思われるので、このぶんだとMA下位者とJ1上位者の入れ替えが繰り返し行われMAメンバーが固定化されるのではないだろうか。

注)*1)平忠正、*2)平経俊、*3)源範頼、*4)平長盛
箱ひげ図(Box-whisker plot)の見方をみると箱の中に引いてある横線は中央値であり、平均値ではない。なるほど、平均値は箱の中心になるのでわざわざ表示する必要はない。中央値ならば、それが中央からずれていれば分布の形が左右対称ではないということが分かる。第3世代(Gen0003)~第5世代(Gen0005)の中央値が下側にあるということは、Tt値が大きい一部のメンバーが平均値を押し上げているということで分布の形がTt値の大きい方に尾を引いているということが分かる。
箱はデータがTtの値が小さい順に並べ4等分したとき、下から4分の1~4分の3の順位のメンバーが入っている値の範囲を示している。
箱から上下に引かれた破線の頂点にある横線は、最小値と最大値を示すが、それは下側境界点と上側境界点の内部にあるデータに限られる。それを外れた値は外れ値となり丸で示す。
下側境界点と上側境界点は箱の高さ(全データの中間的な50%が入るデータの範囲)の1.5倍箱から離れた点である。
MAのグラフを見ると、世代ごとに能力値は高くなる(成長している)。能力値のばらつきが大きくなっている。
外れ値を観察すると外れ値は上側にあり、他より能力がかなり高いメンバーがいるということを示している。ならば、優勝してもいいようなものだが、
第1世代(Gen0001)では、https://ykdn.blog.ss-blog.jp/2019-09-16 源為宗(優勝)、源範頼(優勝同点)、平忠清(優勝同点)だった。 *1の平忠正は7勝8敗と負け越し、*2の平経俊は9勝6敗であった。
第3世代(Gen0003)では https://ykdn.blog.ss-blog.jp/2019-09-16 源為宗(優勝)、源範頼(優勝同点)、平忠清(優勝同点)であり、*3の源範頼は外れ値にふさわしい成績であった。
第4世代(Gen0004) https://ykdn.blog.ss-blog.jp/2019-09-28 では、源為朝が優勝しており、*3の源範頼は9勝6敗、*4の平長盛も9勝6敗と外れ値のメンバーとしては期待外れの成績であった。
第5世代(Gen0005)https://ykdn.blog.ss-blog.jp/2019-10-12 では、平忠盛(優勝)、平正綱(優勝同点)であり、*3の源範頼は5勝10敗と大きく負け越した。
以上能力どおりの成績とはなったおらず、「勝負は時の運」、「勝負は水物」というにふさわしいものとなっている。つまりは、現実でもこのような偶然の力によるものがあってもいいことを意味している。
第10世代(Gen0010)https://ykdn.blog.ss-blog.jp/2019-12-05 では、*4の平長盛は6勝9敗であり、https://ykdn.blog.ss-blog.jp/2019-12-06 「対戦前の実力(能力パラメータ)値による平長盛の平均勝率は0.683126(10.2勝 4.8敗)。乱数による偶然の力が現れている。」としている。
第11世代(Gen0011)https://ykdn.blog.ss-blog.jp/2019-12-13でやっと*4の平長盛が優勝した。でも、今までの結果を踏まえると実力があったから優勝したのか、偶然の力により優勝したのか成績からは区別できない。成績から能力を評価することの難しさをこのシミュレーションは示していると思う。なお、*3の源範頼は11勝4敗の成績であった。
第12世代(Gen0012)https://ykdn.blog.ss-blog.jp/2019-12-20 では、*4の平長盛、*3の源範頼ともに11勝4敗の成績で、優勝は源為朝であった。
以上、外れ値となるような優れた能力であっても優勝できたのは11回中1回のみで優勝同点も11回中1回と能力と成績には強い関連はなかった。
次に上下のクラスとメンバーが入れ替わるJ1について検討する。

注)*1)平重義、*2)平直材、*3)源満末
第5世代(Gen0005) https://ykdn.blog.ss-blog.jp/2019-10-16 の*1の平重義は前世代J2で14勝1敗の成績で優勝し、ここでは10勝5敗であった。
第6世代(Gen0006) https://ykdn.blog.ss-blog.jp/2019-10-27 の*1の平重義は8勝7敗とやっと勝ち越しの成績であった。
第7世代(Gen0007) https://ykdn.blog.ss-blog.jp/2019-11-09 で*1の平重義がやっと優勝して次世代はMAに昇格する。
第8世代(Gen0008)https://ykdn.blog.ss-blog.jp/2019-11-18 は外れ値は*2の平直材であったが、8勝7敗と平凡な成績であった。
第10世代(Gen0010) https://ykdn.blog.ss-blog.jp/2019-12-06 では*3の源満末がJ1から昇格して優勝した。
第11世代(Gen0011)https://ykdn.blog.ss-blog.jp/2019-12-14 では、*3の源満末が大きく離れた値だったが優勝はできなかった。次世代はMAに昇格するのでJ1での外れ値には登場しない。*1の平重義はMAから降格して今世代で優勝し次世代はMAに再昇格する。
J1は成績優秀者がMAに昇格することで外れ値が消える傾向にある。
*1の平重義が良い成績をなかなか上げられずMAに昇格できなく3世代連続して外れ値として登場し、またMAから陥落することによりJ1では能力が外れ値となり11回中4回も登場した。
MAとJ1のグラフを重ねて比較する。

M1とJ1との差が徐々に開いてきた。能力が低くMAから降格するべき者は既に降格してしまっていると思われるので、このぶんだとMA下位者とJ1上位者の入れ替えが繰り返し行われMAメンバーが固定化されるのではないだろうか。
Gen0010(08)F検定を勝敗分布に使う [確率統計]
前回ハートレイ検定でGen0001~Gen0010をまとめて検定すると等分散の仮定が棄却された。ではどの世代で分散に差があったのか
(01) Gen0001とGen0002を比較
(02) Gen0001とGen0003を比較
...
(09) Gen0001とGen0009を比較
(10) Gen0002とGen0003を比較
(11) Gen0002とGen0004を比較
...
(45) Gen0009とGen0010を比較
こんなに沢山比較をすると偶然有意差がでるのは当たり前で「ボンフェローニ補正」を使わなければならない。上の例では45検定あるのだから5%の有意水準で行う検定では両側検定なので0.05÷2÷45≒0.00056を各検定の有意水準とするということ。有意水準1%なら0.00011にする。
でも、予想では、能力値の成長とメンバー入れ替えのため少しずつ分布に差が出て、そのうち定常状態になるというものであるから取り敢えずGen0001の初期値のパラメータによる対戦成績と次世代以降の対戦成績の分散に差があるかどうかを調べたいので両側検定をする。
(01) Gen0001とGen0002を比較
(02) Gen0001とGen0003を比較
...
(09) Gen0001とGen0009を比較
をする。従って0.05÷2÷9≒0.0028又は0.01÷2÷9≒0.00056を各検定の有意水準とする
Rで計算してみると
var.test(Gen0001, Gen0002)
F = 0.48387, num df = 29, denom df = 29, p-value = 0.05519
var.test(Gen0001, Gen0003)
F = 0.51331, num df = 29, denom df = 29, p-value = 0.07769
var.test(Gen0001, Gen0004)
F = 0.50562, num df = 29, denom df = 29, p-value = 0.07131
var.test(Gen0001, Gen0005)
F = 0.26214, num df = 29, denom df = 29, p-value = 0.000553 (*)
var.test(Gen0001, Gen0006)
F = 0.75419, num df = 29, denom df = 29, p-value = 0.4521
var.test(Gen0001, Gen0007)
F = 0.22095, num df = 29, denom df = 29, p-value = 0.0001126 (**)
var.test(Gen0001, Gen0008)
F = 0.36388, num df = 29, denom df = 29, p-value = 0.008175
var.test(Gen0001, Gen0009)
F = 0.39823, num df = 29, denom df = 29, p-value = 0.01566
var.test(Gen0001, Gen0010)
F = 0.34884, num df = 29, denom df = 29, p-value = 0.005947
となった。 p値の右側に (*) があるのは、0.05÷2÷9≒0.0028で有意、 (**) は0.01÷2÷9≒0.00056でも有意を示す。
頻度グラフを再掲する。
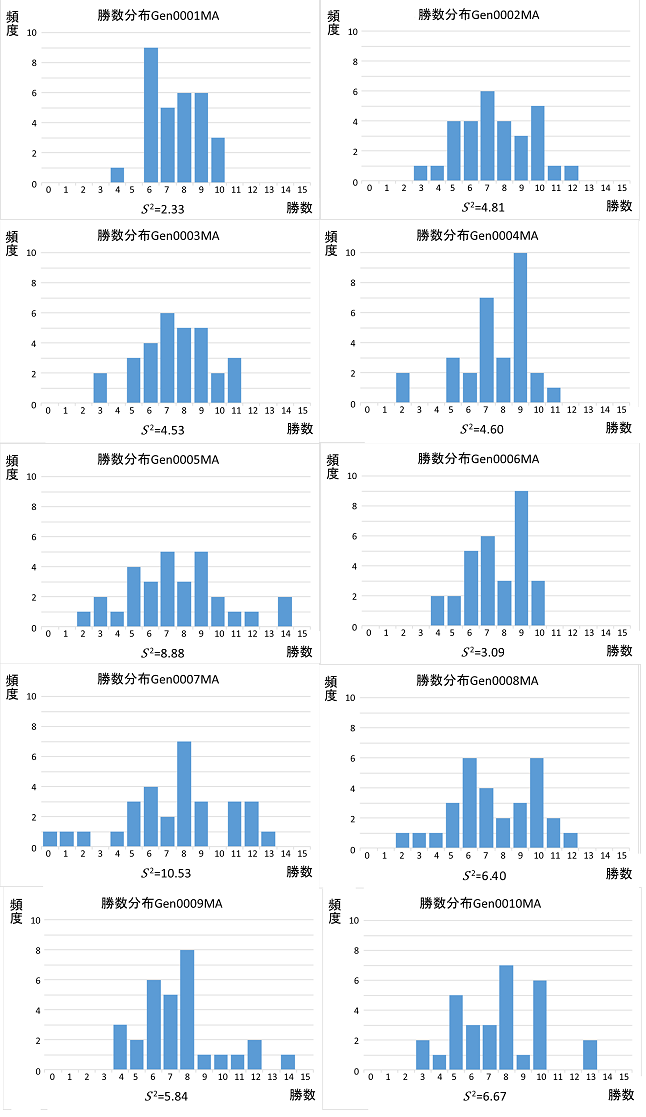
むう。これでは偶然かどうか判断しきれない。予想では少しずつ分布に差が出て、そのうち定常状態になるのだから途中から有意差が連続して出てほしい。そうでなければ、たまたま出たのかどうか区別できない。
シミュレーションでは対戦前の能力値が分かっている。対戦前の能力値分布で分散に差が出ているはずなのでそれが成績にどう反映されるかを統計学的に検討したかったのだが、統計学は役に立っていないように思われる。
そもそも、能力値の差が微小のため成績に顕著な差が現れていないという可能性もある。
偶然の力で優勝している例を見てきており、Gen0007MA序列15位源頼賢の15戦全敗も偶然の力による(対戦前の実力(能力パラメータ)値による源頼賢の平均勝率は0.379139( 5.7勝 9.3敗)。これで全敗するとは意外だった。)と思われるのだから、能力値が成績にあまり強く関与していないことを示しているのかもしれない。
取り敢えず今後シミュレーションを重ねて、成績分布に大きな差が出てきたときに宮城リョータ視点で能力値の分布を検討してみる。
(01) Gen0001とGen0002を比較
(02) Gen0001とGen0003を比較
...
(09) Gen0001とGen0009を比較
(10) Gen0002とGen0003を比較
(11) Gen0002とGen0004を比較
...
(45) Gen0009とGen0010を比較
こんなに沢山比較をすると偶然有意差がでるのは当たり前で「ボンフェローニ補正」を使わなければならない。上の例では45検定あるのだから5%の有意水準で行う検定では両側検定なので0.05÷2÷45≒0.00056を各検定の有意水準とするということ。有意水準1%なら0.00011にする。
でも、予想では、能力値の成長とメンバー入れ替えのため少しずつ分布に差が出て、そのうち定常状態になるというものであるから取り敢えずGen0001の初期値のパラメータによる対戦成績と次世代以降の対戦成績の分散に差があるかどうかを調べたいので両側検定をする。
(01) Gen0001とGen0002を比較
(02) Gen0001とGen0003を比較
...
(09) Gen0001とGen0009を比較
をする。従って0.05÷2÷9≒0.0028又は0.01÷2÷9≒0.00056を各検定の有意水準とする
Rで計算してみると
var.test(Gen0001, Gen0002)
F = 0.48387, num df = 29, denom df = 29, p-value = 0.05519
var.test(Gen0001, Gen0003)
F = 0.51331, num df = 29, denom df = 29, p-value = 0.07769
var.test(Gen0001, Gen0004)
F = 0.50562, num df = 29, denom df = 29, p-value = 0.07131
var.test(Gen0001, Gen0005)
F = 0.26214, num df = 29, denom df = 29, p-value = 0.000553 (*)
var.test(Gen0001, Gen0006)
F = 0.75419, num df = 29, denom df = 29, p-value = 0.4521
var.test(Gen0001, Gen0007)
F = 0.22095, num df = 29, denom df = 29, p-value = 0.0001126 (**)
var.test(Gen0001, Gen0008)
F = 0.36388, num df = 29, denom df = 29, p-value = 0.008175
var.test(Gen0001, Gen0009)
F = 0.39823, num df = 29, denom df = 29, p-value = 0.01566
var.test(Gen0001, Gen0010)
F = 0.34884, num df = 29, denom df = 29, p-value = 0.005947
となった。 p値の右側に (*) があるのは、0.05÷2÷9≒0.0028で有意、 (**) は0.01÷2÷9≒0.00056でも有意を示す。
頻度グラフを再掲する。

むう。これでは偶然かどうか判断しきれない。予想では少しずつ分布に差が出て、そのうち定常状態になるのだから途中から有意差が連続して出てほしい。そうでなければ、たまたま出たのかどうか区別できない。
シミュレーションでは対戦前の能力値が分かっている。対戦前の能力値分布で分散に差が出ているはずなのでそれが成績にどう反映されるかを統計学的に検討したかったのだが、統計学は役に立っていないように思われる。
そもそも、能力値の差が微小のため成績に顕著な差が現れていないという可能性もある。
偶然の力で優勝している例を見てきており、Gen0007MA序列15位源頼賢の15戦全敗も偶然の力による(対戦前の実力(能力パラメータ)値による源頼賢の平均勝率は0.379139( 5.7勝 9.3敗)。これで全敗するとは意外だった。)と思われるのだから、能力値が成績にあまり強く関与していないことを示しているのかもしれない。
取り敢えず今後シミュレーションを重ねて、成績分布に大きな差が出てきたときに宮城リョータ視点で能力値の分布を検討してみる。
Gen0010(07)ハートレイ検定を勝敗分布に使う [確率統計]
ハートレイの等分散性検定
MAクラスでの対戦成績について勝ち星の分布に世代間おいて差があるかどうか検討してみる。MAクラスのメンバーの能力値は最初は初期設定値であるが、1世代ごと成績下位のメンバーがJ1クラスに陥落し、J1クラスの成績上位メンバーが昇格することにより変動している。
その変動が統計学的に検出できるかどうかを検討する。
平均値は使えない。どの世代でも平均値は7.5勝7.5敗である。中央値も7勝か8勝でこれも使えない。
そこで分散を検討する。
検討前の予想では、能力値の成長とメンバー入れ替えのため少しずつ分布に差が出て、そのうち定常状態になるというものである。
さて、統計学的検討をするまえに度数分布のグラフを作り鑑賞する。

(S2は不偏分散である。)
Gen0007MAが一番バラツキが大きいように見える。これは偶然なのだろうか、又は能力値分布に異常があったのか。統計学的には不偏分散に利用者が定めた有意差があるかどうかを示すだけで、偶然かどうかは分からない。通常ならばそこで終わるのだが、このシミュレーションでは能力値が分かるのだから、偶然かどうかが分かるはずだ。宮城リョータ視点で成績を見ることができるのである。最後の手段としてこれを使う。
グラフを見るとGen0001MAは能力が初期値であるのでこのバラツキを初期値としていいだろう。成長に従って上位下位との差が広がりバラツキも大きくなるだろう。グラフの雰囲気ではGen0001MAは他の世代とバラツキが異なっている気がする。
世代間に分散の差があるかどうかを検定するのには2つの考え方がある。
1 2つの世代を比較し分散の差の有無を検定する
2 複数の世代をまとめて比較し分散の差の有無を検定する
1の方法をGen0001~Gen0010までで具体的に考えると
(01) Gen0001とGen0002を比較
(02) Gen0001とGen0003を比較
...
(09) Gen0001とGen0009を比較
(10) Gen0002とGen0003を比較
(11) Gen0002とGen0004を比較
...
(45) Gen0009とGen0010を比較
こんなに沢山比較をするとき有意水準5%とするのは論外。本当は差がなくても当然のように偶然有意差があると判定されるものが出てくる。有意水準1%でも偶然有意差があると判定されるものが出るだろう。ということは、差が偶然なのかどうか判断できなくなるので検定する意味がない。
こういったとき、多数の検定をするときには「ボンフェローニ補正」が使われる。これは簡単で単に有意水準を検定回数で割るというもの。今回の例では45検定あるのだから5%の有意水準で行う検定では0.05÷45≒0.0011を各検定の有意水準とするということ。有意水準1%なら0.00022にする。
検定を使うとき、
1 本当は有意差があるのに検出されないと困る
2 本当は有意差がないのに検出されると困る
のどちらの立場に立つかで使い分けをする必要がある。今回は、メンバーの能力値に世代間の差がありその結果として成績に差があり、それは偶然の可能性が少ないということを言いたいから2の立場で検定する。
星取表シミュレーションをやってきて偶然の力を目の当たりにしているのでこの立場を採用するのは当然である。
そもそも2の立場でまずGen0001~Gen0010全体で勝ち星の分布に差があるかどうかを検定すれば良い。つまり、どれとどれがと特定できなくてもとりあえず差があるのかないのかを知りたい。平均値はどの世代でも7.5勝7.5敗なので分散の差異を調べるだけでよい。各世代の人数が同数なので「ハートレイの検定」で済む。
ハートレイの検定はGen0001~Gen0010までの勝ち数の各不偏分散について最小値を最大値で割った値(Fmax)を使って検定する。全く各不偏分散に差がなければ最小値と最大値は等しいのでFmax=1となり、最小値と最大値の差が広がるとFmaxが大きくなる。Fmaxの数表を見てそれよりFmaxがそれより大きければ有意差ありとなる。
今回の場合
最小値 2.33
最大値 13.28
Fmax = 5.69957
df(水準内の自由度) = 29
k(水準数)= 10
Fmaxの数表から
上限5%点 (df=30, k=10) 3.27
(df=20, k=10) 4.35
上限1%点 (df=30, k=10) 3.97
(df=20, k=10) 5.57
有意差ありとなった。Gen0001~Gen0010までまとめて検討すると等分散仮定は棄却された。
最初の度数分布グラフを見た段階で等分散ではないという感覚はつかんでいたので統計学的にもその感覚が支持されたということ。
日本シリーズ4連勝(09) [確率統計]
偶然か実力どおりかは分からない
一方が4連勝したからといって実力に大きな差があるとは断定できない。
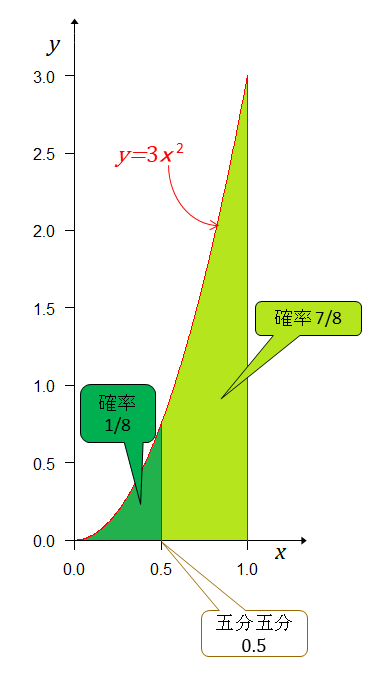
最初に計算したとおり、実力差が無くともその確率は8分の1で0.125もある。
ただ、ベイズの定理を使った主観確率の立場では、対戦前の事前確率が五分五分の実力であっても4連勝後は連勝したチームの実力(相手に対する勝率)は期待値として6分の5で約8割3分の勝率と見積るべきということだ。
対戦前は五分五分と思っていても4連勝後はおおよそ8:2で4連勝したチームが有利だろうと見積もるべきとなる。
ところで、知りたいのは4連勝が偶然か実力どおりだったかということで期待値以上の確率は0.5981であると言われてもしょうがない。とどのつまり結果から確率を計算しても真の実力は分からないということだ。
良く言われることで、「事故の原因がそれである確率は95%ということは分かりましたが、結局この事故はその95%で起きた事故ですか?それとも5%の方ですか」がある。だから、それが分からないから確率なんだけど。統計学は後知恵統計学で予言ではない。確定診断ができるものではない。この辺が理解してもらえないことだ。
 たとえば、サイコロを転がし「1よ出ろ」と言って1が出る確率は6分の1。よくあることで「運がいいな」で終わる。次に「4よ出ろ」と言って4が出る確率も6分の1だが、2回連続して希望の目が出る確率は36分の1で0.0278。確かに珍しいが、これがTV番組なら「流石スター!持ってますね」という流れになる。次に「2よ出ろ」と言って2が出たら、3回目の独立試行の確率は6分の1だが、3回連続希望の目を出す確率は、216分の1(0.0046)となる。ディレクターなら悩むのではないだろろうか。このまま放送するとやらせだと思わないか?今のはNG扱いにしてもう一度振らせるべきではないか。
たとえば、サイコロを転がし「1よ出ろ」と言って1が出る確率は6分の1。よくあることで「運がいいな」で終わる。次に「4よ出ろ」と言って4が出る確率も6分の1だが、2回連続して希望の目が出る確率は36分の1で0.0278。確かに珍しいが、これがTV番組なら「流石スター!持ってますね」という流れになる。次に「2よ出ろ」と言って2が出たら、3回目の独立試行の確率は6分の1だが、3回連続希望の目を出す確率は、216分の1(0.0046)となる。ディレクターなら悩むのではないだろろうか。このまま放送するとやらせだと思わないか?今のはNG扱いにしてもう一度振らせるべきではないか。視聴者の立場では、3連続希望の目が出たとき「やらせだ、編集している」と思うのではないだろうか。確率0.0046だからそう思っても不思議ではない。ところが、3回目に目を外した映像を見たとき視聴者はディレクターの判断で振りなおしさせて目を外させたと思うだろうか、多分思わないだろう。視聴者は結果を見てもそれが真実かどうかは確率論をもってしても正確には判断できない。
しかし、番組制作者側は真実を知っている。確率0.0046の事象が起きたのかそうではないのか。まるで神の視点だ。
宮城リョータ視点
スラムダンクというバスケットボール漫画がある。
主人公の桜木花道(高校1年生)は抜群の身体能力、運動神経を持ち監督に「10年に1人の逸材」と評価されている。桜木花道は高校に入ってからバスケを始めたド素人であるが、中学校からバスケをしているチーム内ライバルの流川楓(これも「10年に1人の逸材」)とプレーしているうちにどんどん上達していく。彼をスカウトし、練習に付き合ってた同学年の女子から彼の上達の速さは「まるで新幹線のよう」と嫉妬された。
 その桜木がインターハイで全国屈指の強豪校のエースプレーヤ沢北栄治(インターハイ後アメリカにバスケ留学する。)に対し素人考えのディフェンスをしたところ、予想外のプレーのため沢北はオフェンスチャージングのファールを取られた。このことで沢北は桜木を警戒することになった。
その桜木がインターハイで全国屈指の強豪校のエースプレーヤ沢北栄治(インターハイ後アメリカにバスケ留学する。)に対し素人考えのディフェンスをしたところ、予想外のプレーのため沢北はオフェンスチャージングのファールを取られた。このことで沢北は桜木を警戒することになった。桜木のチームメイトの宮城リョータは「しめしめ、沢北が警戒している。あのプレーは、10回に1回しか成功しない。その1回が最初に来ただけなのに」とさらに沢北を攪乱する。
沢北は桜木のディフェンスの成功率は結果から推定するしかない。だから警戒する。
宮城リョータは一緒に練習している桜木のプレーから成功率を10分の1と知っている。
この宮城リョータ視点を体験するシミュレーションを考えた。
星取表シミュレーション
 プレーヤの実力をパラメータで与え対戦させる。そこで優勝したプレーヤがまぐれで優勝したのか実力抜群だったのかをパラメータを調べると分かる。大相撲なら15戦全勝優勝した力士と他の力士とはどの程度の実力差があったのか、まぐれだったのかを結果を見た後で、パラメータを調べると宮城リョータ視点で知ることができる。
プレーヤの実力をパラメータで与え対戦させる。そこで優勝したプレーヤがまぐれで優勝したのか実力抜群だったのかをパラメータを調べると分かる。大相撲なら15戦全勝優勝した力士と他の力士とはどの程度の実力差があったのか、まぐれだったのかを結果を見た後で、パラメータを調べると宮城リョータ視点で知ることができる。こういったプログラムを作って次回以降楽しみたい。
日本シリーズ4連勝(08) [確率統計]
ベイズ推定の逐次合理性を利用して4連勝まで事後確率を計算してみる
ベイズ推定の逐次合理性というものがあって、順々に計算できるらしい。つまり
事前分布→事後分布
として
対戦前→1勝後
1勝後→2連勝後
2連勝後→3連勝後
3連勝後→4連勝後
と事前分布を逐次更新していって計算できるとのこと。
対戦前の状態を示す。
Aチームの実力(勝率)がであるときの確率密度(確率を計算するための数値で確率とは違う)をとすると事前分布は下図のとおり。
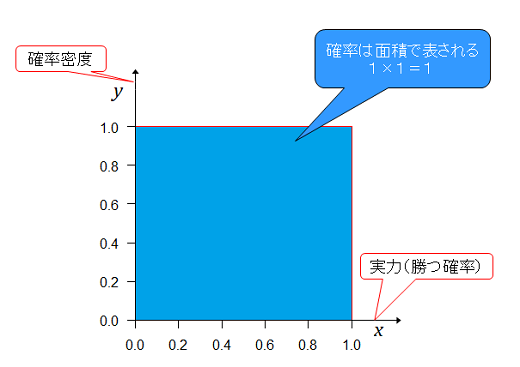
1勝後
対戦後は、それぞれの実力が現れる度合(確率密度)での勝つ確率を計算する。それぞれの実力が現れる度合(確率密度)は一様分布で だから、実力(勝つ確率、勝率)をかけて となる。 グラフにすると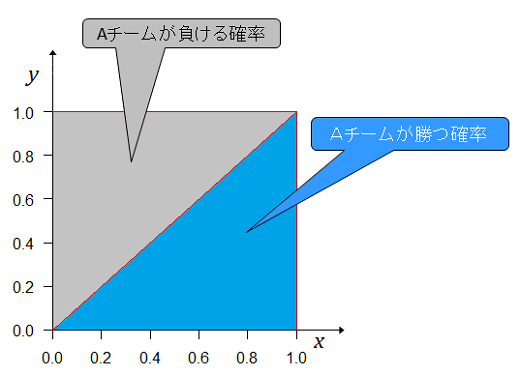
下の青色の部分がAチームが勝った確率で上側の灰色の部分がAチームが負けた確率になる。青色の三角形の部分の面積はAチームの実力(勝つ確率)が0~1での第1戦目に勝つ(勝った)確率となるが、面積は底辺×高さ÷2となるので である。
確率分布とするためには、全事象の確率を1とするために正規化という作業をする。
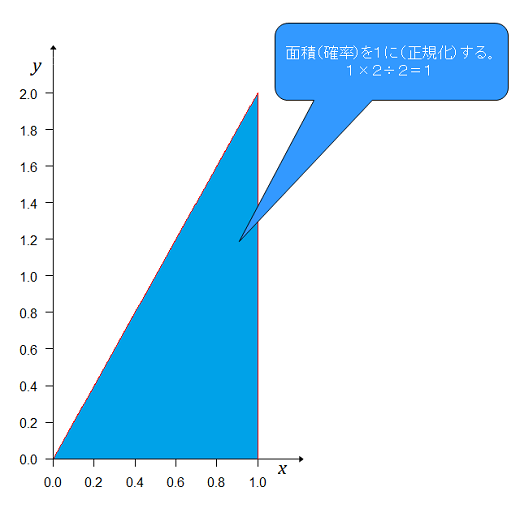
式は これが1勝後の事後分布かつ2戦目の事前分布となる。
2勝後
2戦目は、事前分布であるそれぞれの実力が現れる度合(確率密度)での勝つ確率を計算する。勝つ確率はそれぞれの実力だから2連勝の起こる確率は、事前分布に勝つ確率を掛けて となる。 グラフにすると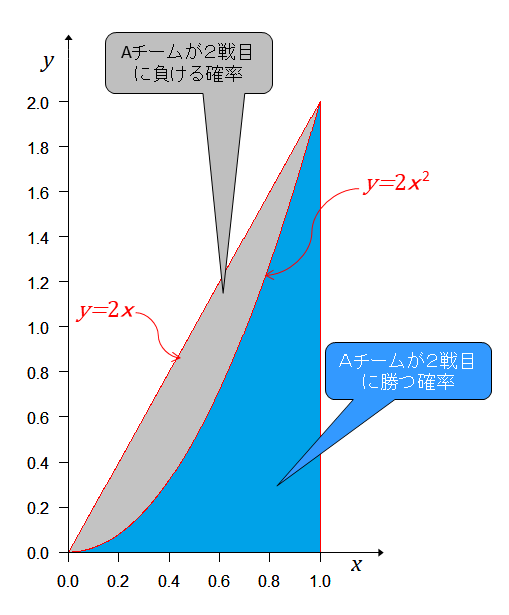
青色の部分がAチームが2戦目も勝った確率で上の灰色の部分がAチームが2戦目で負ける確率となる。青色の部分の面積は 正規化するためには、を掛ければ良いから となる。
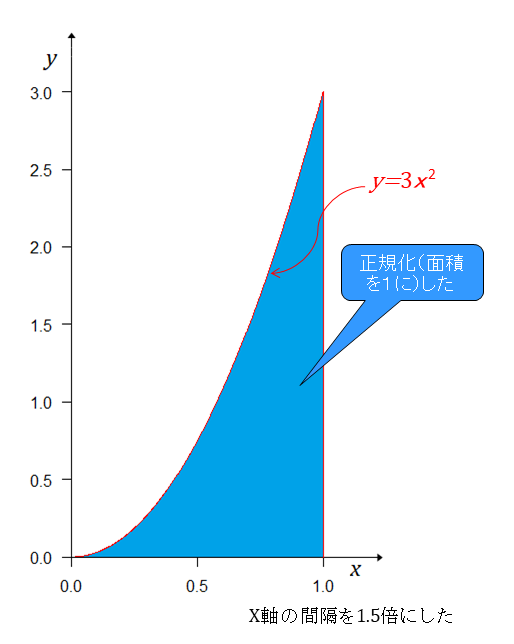
これが、事後分布となる。
3勝後
3戦目は、事前分布であるそれぞれの実力が現れる度合(確率密度)での勝つ確率を計算する。勝つ確率はそれぞれの実力だから3連勝の起こる確率は、事前分布に勝つ確率を掛けて となる。グラフにすると
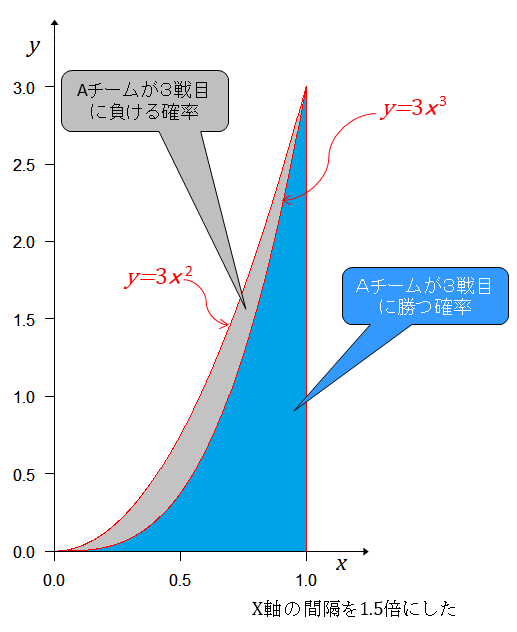
青色の部分がAチームが3戦目も勝った確率で上の灰色の部分がAチームが3戦目で負ける確率となる。青色の部分の面積は 正規化するためには、を掛ければ良いから
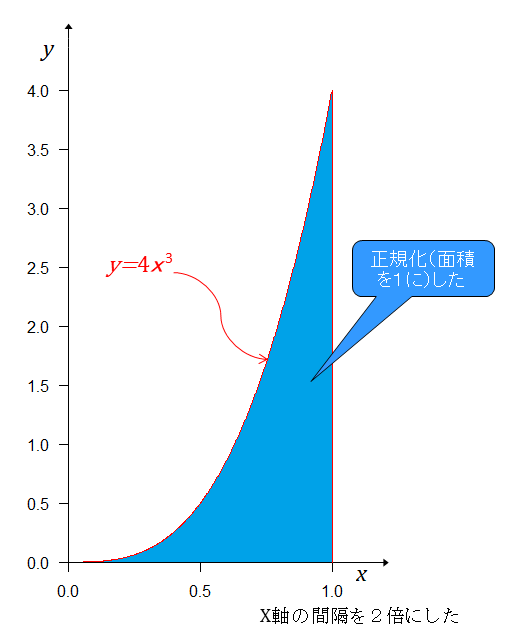
これが、事後分布となる。
4勝後
4戦目は、事前分布であるそれぞれの実力が現れる度合(確率密度)での勝つ確率を計算する。勝つ確率はそれぞれの実力だから4連勝の起こる確率は、事前分布に勝つ確率を掛けて となる。 グラフにすると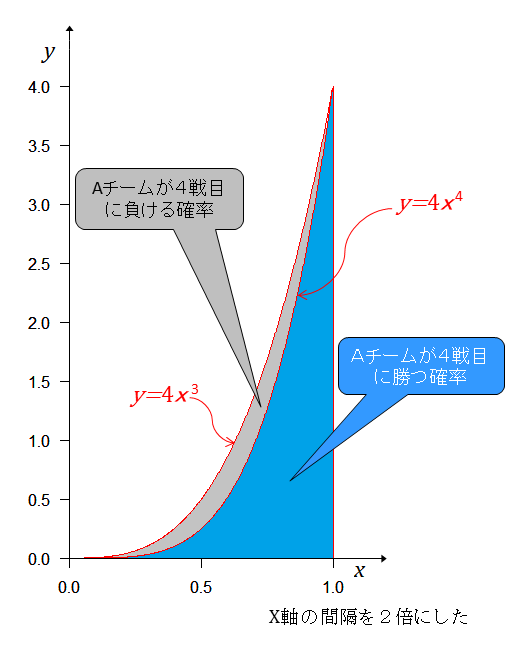
青色の部分がAチームが4戦目も勝った確率で上の灰色の部分がAチームが4戦目で負ける確率となる。青色の部分の面積は 正規化するためには、を掛ければ良いから
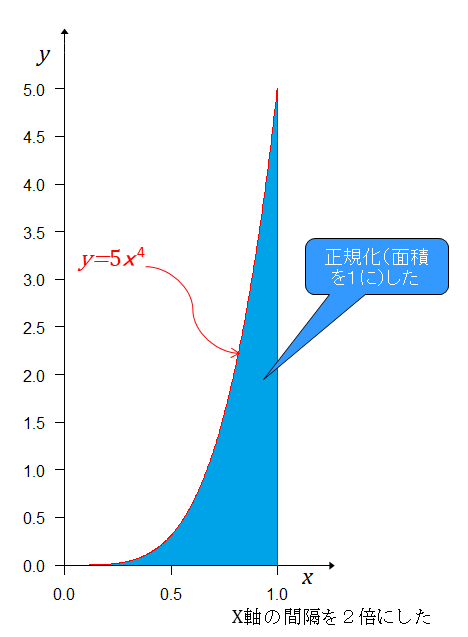
これが、事後分布となる。
当たり前だが、前回の対戦前の事前確率からいきなり4連勝したときの事後確率分布と同じ式になっている。
日本シリーズ4連勝(07) [確率統計]
2連勝から4連勝までのAチームの実力について事後確率分布を計算してみる
前回の復習
まず、対戦前の事前分布を一様分布としたときの確率分布関数や各統計量は前回計算したとおり…… 確率密度
…… Aチームの実力(勝つ確率)
…… 事前分布
…… 期待値
…… 確率を二等分するの値。自己流。中央値に相当するか?
…… Aチームが強い確率が弱い確率の何倍か。自己流。オッズ比に相当するか?
続いて、1勝後の事後確率分布関数や各統計量は前回計算したとおり
…… 事後分布
上を正規化(1勝した確率の合計を1に調整する)すると
…… 正規化後の分布
…… 期待値
…… 確率を二等分するの値。自己流。中央値に相当するか?
…… Aチームが強い確率が弱い確率の何倍か。自己流。オッズ比に相当するか?
2連勝後の事後分布(1)
初期状態の事前分布はAチームが2連勝する確率は だから これが2連勝後のグラフとなる。事前分布とこれを重ねると
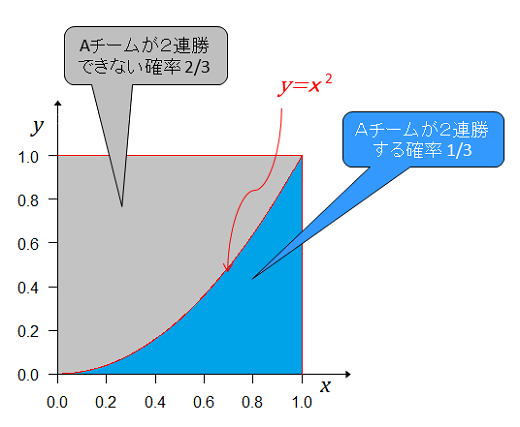
青の部分の面積は 正規化すると(青の部分の面積を1にする。すなわち、全事象の確率(2連勝の確率の合計)を1にする。) これが、事後分布となる。
2連勝後の事後分布(2)
これをベータ分布で考えると、ベータ分布の一般式は下記のとおりで ここで、…… 右辺での確率密度
…… 全事象確率を1にするための調整定数
…… Aチームの実力(勝つ確率)
…… Aチームが負ける確率
…… Aチームの勝利数
…… Aチームの敗北数
2勝0敗だから としてやる。
前記と同様に全事象の確率が1となるようにすると事後分布は ベータ分布の期待値は である。
期待値以下の面積(確率)は 期待値以上の面積(確率)は Aチームの実力(勝率)が期待値以上である確率は期待値以下の確率の1.37倍大きい。
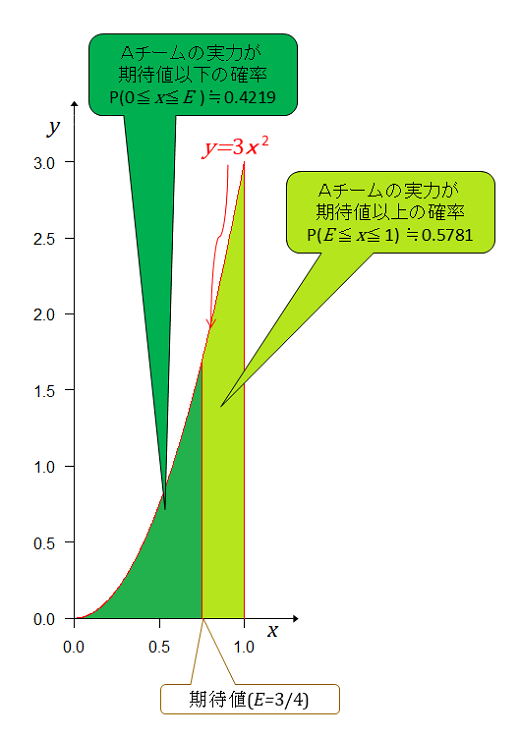
左右の確率が等しくなる点は
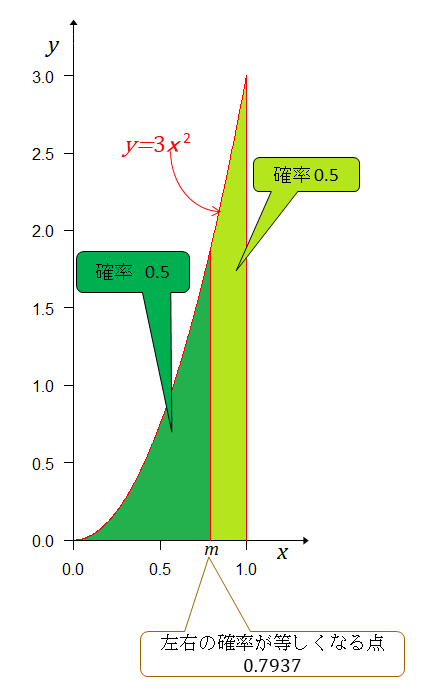
次にAチームの実力(勝率)がBチームより強いか、弱いかを確率で示す。 が五分五分だから左(弱い)右(強い)に分けて確率を求める。 だから その結果が下図。
2連勝した時点でAチームの方が強い確率が弱い確率よりも7倍も大きくなる。ベイズの定理を使って事後確率分布を計算していると自分では思っているのだが、それが正しいと考えれば、オッズ比(?)は7倍だから3戦目はAチームが負ける方に1万円賭け、Aチームが負けると8万円戻るという賭けとAチームが勝つ方に7万円賭け、Aチームが勝つと8万円戻るという賭けが平等ということになる。素人考えでは、負ける方に賭けるのが有利に感じる。
3連勝した
初期状態の事前分布はAチームが3連勝する確率は だから これが3連勝後のグラフとなる。事前分布とこれを重ねると
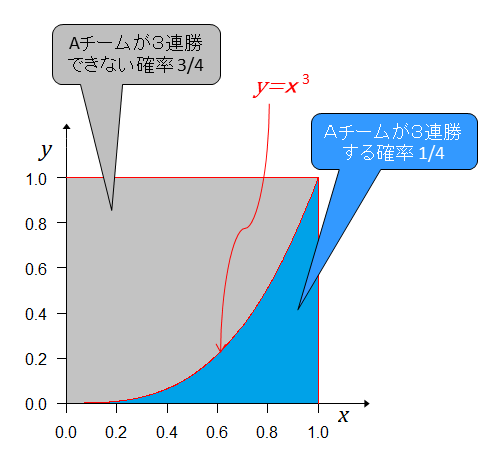
青の部分の面積は 正規化すると(青の部分の面積を1にする。すなわち、全事象の確率を1にする。) これが、事後分布となる。
3連勝後の事後分布(2)
これをベータ分布で考えると、 3勝0敗だから としてやる。前記と同様に全事象の確率が1となるように正規化すると事後分布は となり、ベータ分布の期待値は である。
期待値以下の面積(確率)は 期待値以上の面積(確率)は Aチームの実力(勝率)が期待値以上である確率は期待値以下の確率の1.44倍大きいが、2連勝と3連勝では大して変わらない。
左右の確率が等しくなる点は
Aチームの実力(勝率)がBチームより強いか、弱いかを確率で示す。 の左(弱い)右(強い)に分けて確率を求める。 だから その結果が下図。
4連勝した
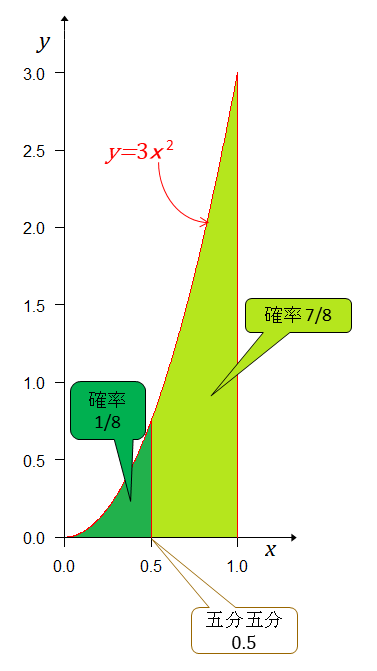
初期状態の事前分布はAチームが4連勝する確率は だから これが4連勝後のグラフとなる。事前分布とこれを重ねると
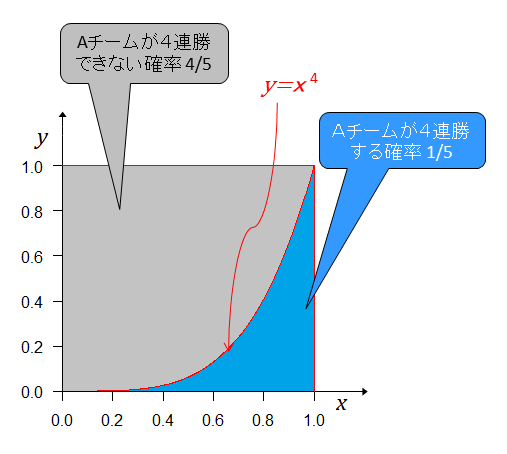
青の部分の面積は 正規化すると(青の部分の面積を1にする。すなわち、全事象の確率を1にする。) これが、事後分布となる。
4連勝後の事後分布(2)
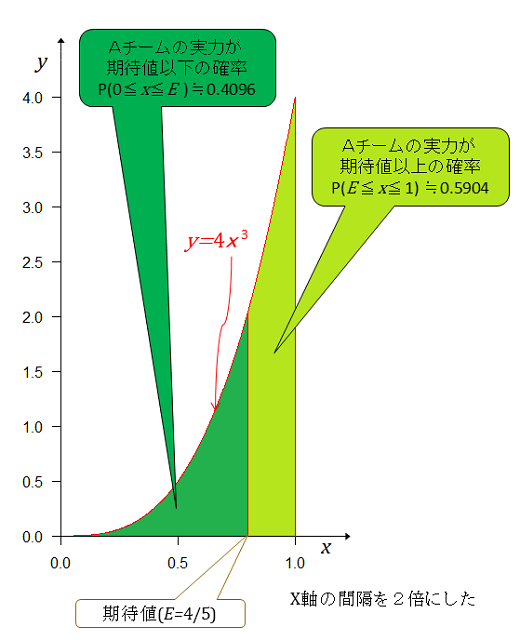
これをベータ分布で考えると、 4勝0敗だから としてやる。 前記と同様に全事象の確率が1となるように正規化すると事後分布は となり、ベータ分布の期待値は である。期待値以下の面積(確率)は 期待値以上の面積(確率)は Aチームの実力(勝率)が期待値以上である確率は期待値以下の確率の1.49倍大きいが、伸びは2連勝、3連勝、4連勝となるごとに鈍化している。
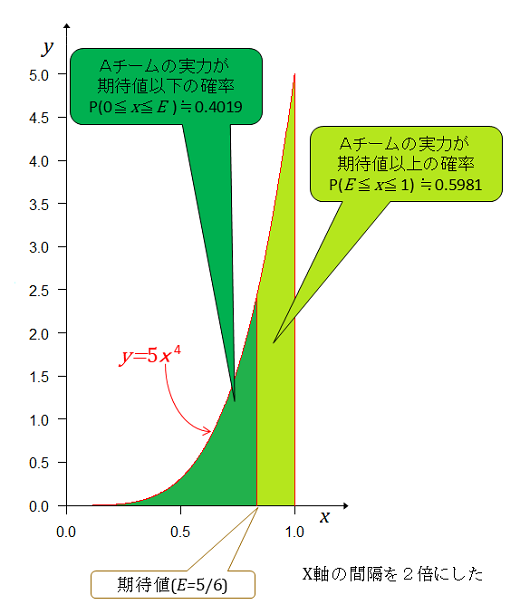
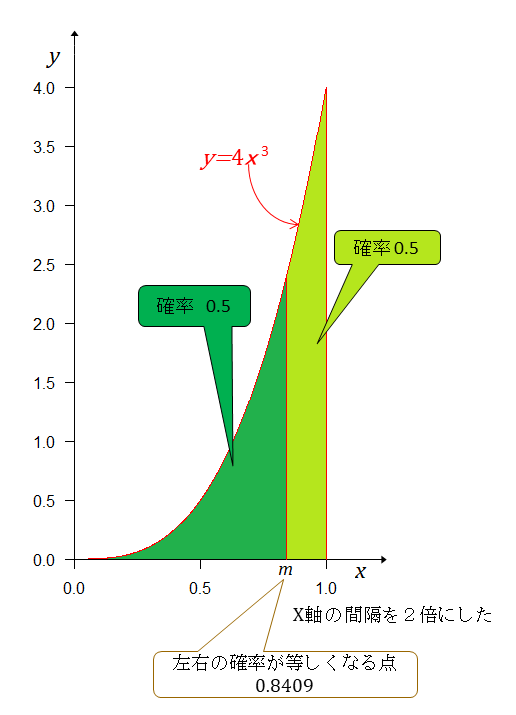
左右の確率が等しくなる点は
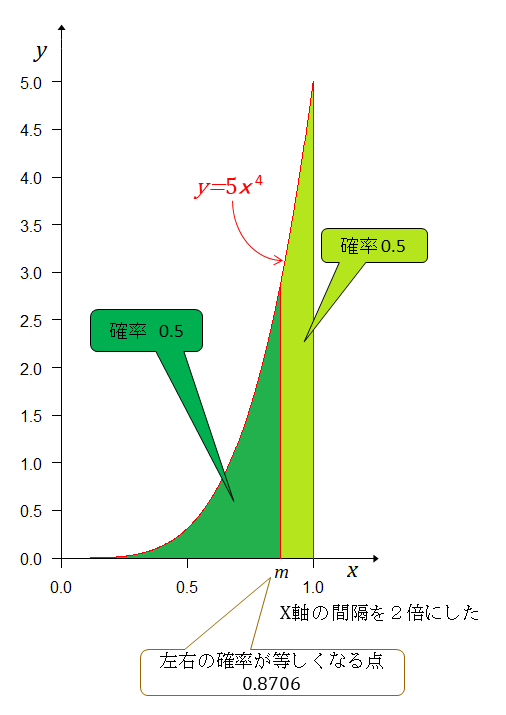
Aチームの実力(勝率)がBチームより強いか、弱いかを確率で示す。 の左(弱い)右(強い)に分けて確率を求める。 だから その結果が下図。
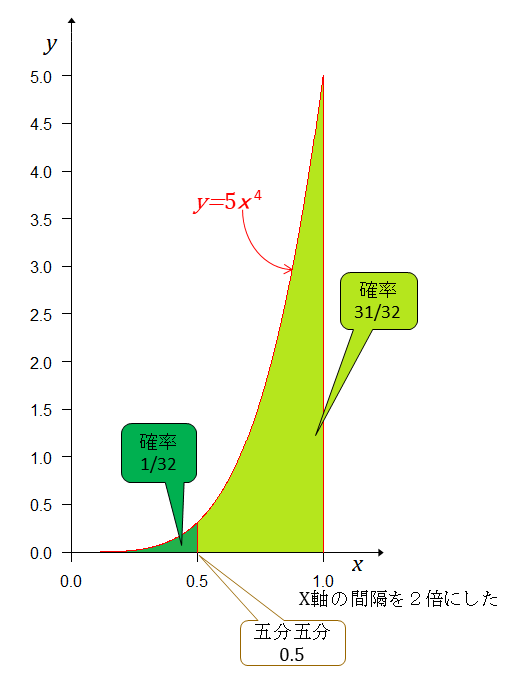
Aチームの方が強い確率が約97%(0.96875)だということになる。実力が互角ならどちらかが4連勝する確率は16分の2で0.125となるにもかかわらず、ベイズの定理に従って(自分ではそう思っている)計算したら、4連勝したら五分五分ではない確率が約97%であるというわけだ。
腑に落ちない。
ベイズ推定の逐次合理性
今回は、対戦前の事前確率分布から1勝、2連勝、3連勝、4連勝後の事後確率分布を計算したが、ベイズ推定の逐次合理性というものがあって、順々に計算できるらしい。つまり
事前分布→事後分布
として
対戦前→1勝後
1勝後→2連勝後
2連勝後→3連勝後
3連勝後→4連勝後
と事前分布を逐次更新していって計算できるとのこと。
次回、これで計算してみる。
日本シリーズ4連勝(06) [確率統計]
Aチームの実力を連続変数として計算してみる
Aチームの実力を3パターンで計算してみたが、全部を網羅して計算したい。そうすると、Aチームの実力の期待値が計算できたり、0.5~0.6となる確率とか0.5以下のときの確率とか自由自在に計算できる。ベイズの定理の復習と適用
まず、ベイズの定理の復習 各項目の意味は、…… Bという事象が起こったときに事象Aが起こる確率
…… Aという事象が起こったときに事象Bが起こる確率
…… Aという事象が起こる確率
…… Bという事象が起こる確率
これを今回の日本シリーズ4連勝に当てはめてみる。変数名を連想しやすく変える。
各項目の意味は、
…… Aチームが1勝、2連勝、3連勝もしくは4連勝したときに、Aチームの実力がである確率
…… Aチームの実力がのとき、勝つ確率(それぞれの計算で1勝、2連勝、3連勝、4連勝する確率)
…… Aチームの実力(勝率)がである確率
…… Aチームが勝つ確率(それぞれの計算で1勝、2連勝、3連勝、4連勝する確率)
…… これを事前確率といって、事前確率(それぞれの実力に対する勝つ確率)を仮定(計算)しておいて
…… これを事後確率といって、対戦結果をみて真(?)の実力を求める
多分、この解釈でいいと思う。
事前分布をグラフにしてみる
確率を連続変数として計算してみる。 まず、分かりやすくするため、Aチームの実力がであるときの確率密度(確率を計算するための数値で確率とは違う)をとして事前分布を図示する。連続変数とした段階で事前確率は事前(確率)分布、事後確率は事後(確率)分布となり期待値(平均値と言ってもいいか?)や、実力の範囲の確率(例えば実力が0.5~1とか)が計算できる。
一様分布だからその式は
このグラフ(一様分布)はベータ分布でも描けるのだが、ベータ分布の一般式は下記のとおり。 ここで、
…… 右辺での確率密度
…… 全事象確率を1にするための調整定数
…… Aチームの実力(勝つ確率)
…… Aチームが負ける確率
…… Aチームの勝利数
…… Aチームの敗北数
対戦前の事前分布を表すのだから、勝利数も敗北数も0にするために
として となる。
ベータ分布にして便利な点は期待値(平均値、多分加重平均値だと思う)を簡単に計算できることがある。 ベータ分布の期待値の式は なので、一様分布の場合は である。
1勝後の事後分布(1)
なら必ず負けるので 、 なら必ず勝つので 、 なら勝敗の確率は五分五分なので となる。つまり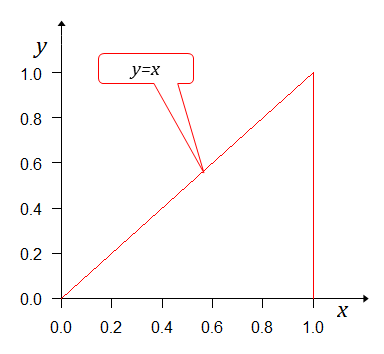
となる。
事前分布と重ねると

下の水色の部分がAチームが勝った確率で上側の灰色の部分がAチームが負けた確率になる。水色の三角形の部分の面積はAチームの実力(勝つ確率)が0~1での第1戦目に勝つ(勝った)確率となるが、面積は底辺×高さ÷2となるので である。
第2戦へは勝った方だけが行くので、勝った方の確率の合計が1となるように調整(正規化)すると下図のとおり

式は これが1勝後の事後分布となる。
1勝後の事後分布(2)
念のためベータ分布でも計算してみる。1勝0敗だから としてやる。上と同様に全事象の確率が1となるようにすると 期待値は である。
1勝しただけで、Aチームの実力(勝率)の期待値が となるが、感覚的にはたった1勝でAチームはBチームに対して期待値で約6割7分の勝率を見込むとは盛りすぎではないかと思うが、ベイズ流の確率計算ではこうなるのでしょうがない。ベイズ流の主観確率では対戦前の事前確率分布の期待値が五分五分と思ってたが、対戦後は事後分布の期待値が約6割7分だと思うべきだとなる。
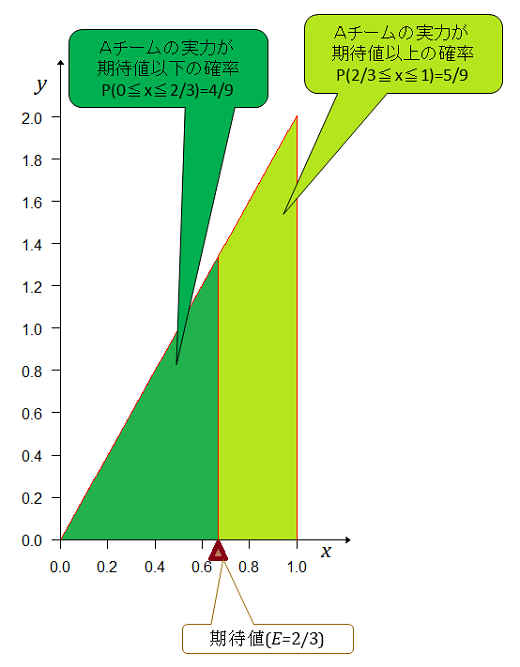
この期待値というのは、平均値ではなく加重平均(重心)であり上のように期待値を支点としてやじろべえを作ると左右が釣り合うということになる。図で見ると感覚的に釣り合うように思えない。左に傾きそう。
で、左側が期待値 以下の確率 、右側が期待値 以上の確率 はそれぞれ、 である。Aチームの実力(勝率)が期待値以上の確率の方が期待値以下よりも大きい(1.25倍)。こうなると期待値というのが感覚的に納得できない。
素人考えでは期待値は平均値となるべきで、図の左右の面積(確率)が等しい点、つまり確率0.5となる点ではなかろうかと。だから三角形の面積の計算で底辺×高さ÷2=0.5。そうなる底辺をとする。高さはだから。
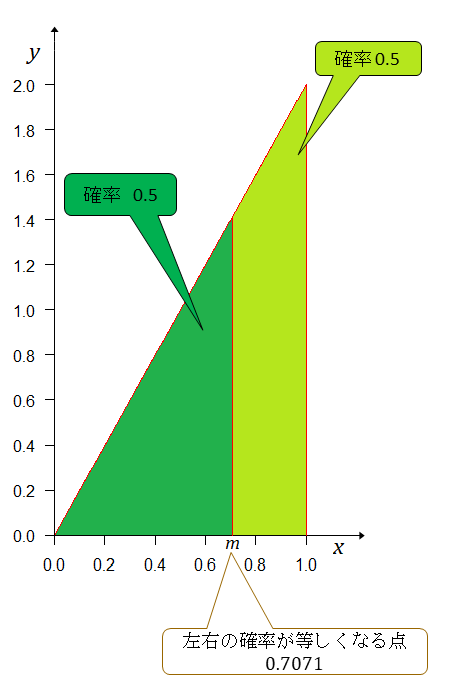
は、いったい何なのだろう。平均値とは言えないのだろうな。中央値(median)かな?分からない。計算結果は、意外にもの方が、期待値よりもAチームが強いと見積もられている。
別の考えをして、今度はAチームの実力(勝率)がBチームより強いか、弱いかを確率で示すと が五分五分だから左(弱い)右(強い)に分けて確率を求める。その結果が下図。
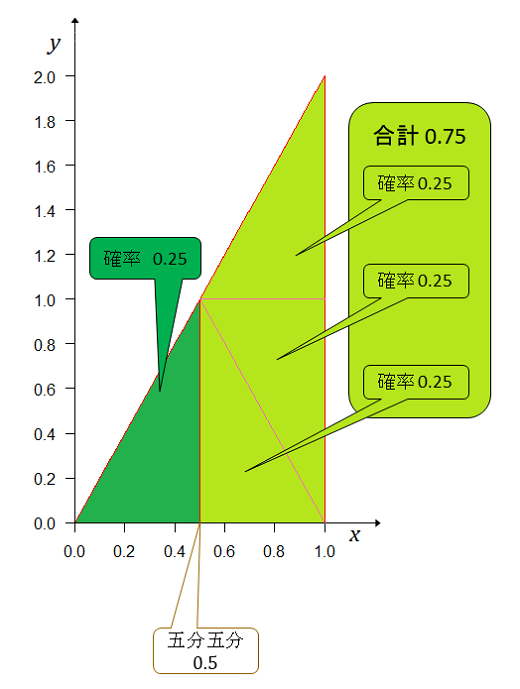
たった1勝しただけでAチームの方が強い確率が弱い確率よりも3倍も大きくなる。たった1勝なのに。ベイズの定理を使って事後確率分布を計算していると自分では思っているのだが、この計算結果は、ちょっと感覚的になじめない。
取り敢えず、今回はここまで。次回2連勝から4連勝までの事後確率を計算する。
日本シリーズ4連勝(05) [確率統計]
Aチームの実力がaの確率を図で整理してみる
前回の計算結果を図にして復習してみる。対戦前の事前確率分布から4連勝後までの確率分布を図にしてみた
w520.png)
w520-a502b.png)
w520-f43bc.png)
w520-45161.png)
w520-26fe0.png)
本を読むと確率を面積で示すのが流儀だと分かった。全体の面積を1として各部分の面積を計算するとその面積が確率の値となる。かなり、分かりやすい工夫だと思う。 5枚の図を見ると、4連勝後は、6・4でAチームの方が強い確率が五分五分や4・6よりも高い確率(面積が広い)となっている。それでも逆にAチームの方が弱いのに4連勝する確率が1割強もある。こんなとき、「Aチームに勢いがありましたね。」なんて解説者がしたり顔でいうけど、勢いというのは単なる偶然のことかもしれないということがグラフで分かる。
Aチームの実力aを連続変数にして事前分布を検討してみる
3通りの計算はできた。次は9通りなんて中途半端なことはせずaを連続変数として計算してみる。
まず分布の検討から。対戦前はAチームが勝つか負けるかの確率は分からない。こういったときベイズ流ではどちらかが強いとかの事前情報がないのだから期待値(平均値又は重心)は中立の値で0.5となる分布を事前確率分布として仮定する。また、0から1までの間でaどのように分布するのかの情報もないので均等に分布するとして下図のような一様分布を仮定する。
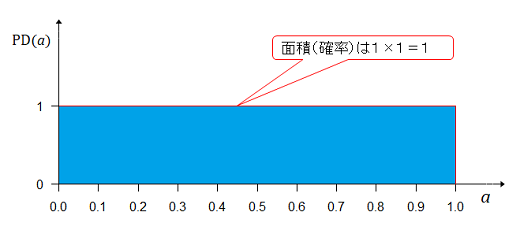
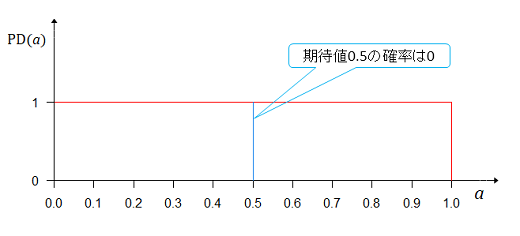
期待値0.5のところの高さは1であるが、これは期待値0.5の確率ではない。この高さのことを確率密度というそうだ。確率を計算するには面積を求めるのだが、幅が0だから面積は1×0=0である。 ピンポイントで確率は計算できない。
しかし、期待値0.45~0.55ならば下図のとおり
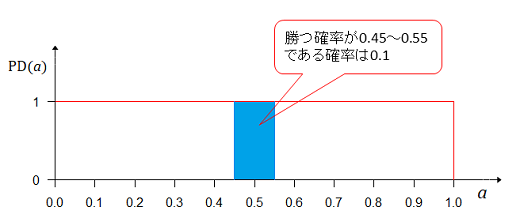
確率は1×0.1=0.1と計算できる。
一様分布は対戦チームの実力が0から1までなのだから、対戦チームがプロ野球から草野球まで玉石混交状態であるときにモデルとして適当と思われる。しかし、日本シリーズとかのプロの頂上決戦では各チームの勝つ確率が一様分布では事前分布として不適当ではないか。 一様分布は特殊な分布だと考えられる。一様分布している自然現象は知っている限りでは電気的ノイズのようなもので乱数の発生装置として利用していると聞いたことがある。沢山データをとってそれが一様に並ぶなんて予めデータに細工をしておかねばできないようにも思える。一様分布は胡散臭い分布が感想。
ならば、平均値0.5の正規分布はどうだろうか。
平均値0.5の正規分布といっても、標準偏差(sd)によって分布の形が変わる。下図に標準偏差がsd=0.05~0.08でグラフを描いてみた
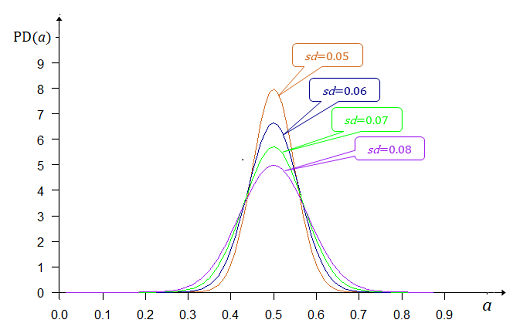
sd0.05w520.png)
sd0.06w520-67463.png)
sd0.07w520-f85bf.png)
sd0.08w520-27aef.png)
さて上の分布のうちどれを事前分布として採用すべきか。 そもそも、色々な統計量は正規分布に近似できるものが多い。例えば、身長、体重、テストの成績、実験の計測値等々。それらは、過去にデータをとってヒストグラム作って確かめられている。この経験則があるので少数のデータでも統計学的な判断ができる。 しかし、日本シリーズ4連勝ではこれができない。
日本シリーズ4連勝では元になる実力、勝つ確率をあらかじめ測定できず、ヒストグラムは作れるわけもない。対戦前に勝つ確率を実測できないのなら、正規分布をしているかもしれないが、標準偏差は当然分からず適当な事前分布を仮定できない。
どうせ適切な分布を仮定できないのなら、計算に便利な一様分布を使うというのもありかなと思う。統計学の専門家はこんなところで思い悩まず一様分布を仮定して利用するのだと思う。

青色の部分の面積は高さ×幅で1×1=1である。
勝負の確率が0.5(五分五分)の確率はというと次の図で
勝負の確率が0.5(五分五分)の確率はというと次の図で

期待値0.5のところの高さは1であるが、これは期待値0.5の確率ではない。この高さのことを確率密度というそうだ。確率を計算するには面積を求めるのだが、幅が0だから面積は1×0=0である。 ピンポイントで確率は計算できない。
しかし、期待値0.45~0.55ならば下図のとおり

確率は1×0.1=0.1と計算できる。
一様分布は対戦チームの実力が0から1までなのだから、対戦チームがプロ野球から草野球まで玉石混交状態であるときにモデルとして適当と思われる。しかし、日本シリーズとかのプロの頂上決戦では各チームの勝つ確率が一様分布では事前分布として不適当ではないか。 一様分布は特殊な分布だと考えられる。一様分布している自然現象は知っている限りでは電気的ノイズのようなもので乱数の発生装置として利用していると聞いたことがある。沢山データをとってそれが一様に並ぶなんて予めデータに細工をしておかねばできないようにも思える。一様分布は胡散臭い分布が感想。
ならば、平均値0.5の正規分布はどうだろうか。
平均値0.5の正規分布といっても、標準偏差(sd)によって分布の形が変わる。下図に標準偏差がsd=0.05~0.08でグラフを描いてみた

しつこいけれど、実力の予想を五分五分と四分六で考えているのでAチームが勝つ確率を0.4~0.6の間の確率が高いとみて各標準偏差のとき勝つ確率が0.4~0.6に入る確率(P(z))を計算してみた。結果は下図のとおり。
sd0.05w520.png)
sd0.06w520-67463.png)
sd0.07w520-f85bf.png)
sd0.08w520-27aef.png)
さて上の分布のうちどれを事前分布として採用すべきか。 そもそも、色々な統計量は正規分布に近似できるものが多い。例えば、身長、体重、テストの成績、実験の計測値等々。それらは、過去にデータをとってヒストグラム作って確かめられている。この経験則があるので少数のデータでも統計学的な判断ができる。 しかし、日本シリーズ4連勝ではこれができない。
日本シリーズ4連勝では元になる実力、勝つ確率をあらかじめ測定できず、ヒストグラムは作れるわけもない。対戦前に勝つ確率を実測できないのなら、正規分布をしているかもしれないが、標準偏差は当然分からず適当な事前分布を仮定できない。
どうせ適切な分布を仮定できないのなら、計算に便利な一様分布を使うというのもありかなと思う。統計学の専門家はこんなところで思い悩まず一様分布を仮定して利用するのだと思う。
日本シリーズ4連勝(04) [確率統計]
【修正版 2019.08.06】
Aチームの実力がaの確率を計算してみる
今までAチームの実力がaであるときの4連勝決着確率又は4連勝及び4連敗決着確率を計算してきたが、逆に4戦で決着したときにAチームの実力がaである確率を計算してみる。ベイズの定理というもので計算できるのだが、ここは地道に計算してみる。3パターンで考える4連勝決着のときのAチームの実力
対戦が始まる前は、AチームとBチームの実力が次の3通りのいずれかでどれが一番確からしいかとかは分からず、皆平等だと考える。Aチームの勝つ確率を の3通りでそれらの確率はと考える。この予め仮定したの確率のことを事前確率というはずだ。
Aチームが1勝した後
1戦目でAが勝ったとき、 のそれぞれで考える。まず のとき勝つ確率はだがこれを こう書く。文章にすると、Aチームの実力が0.6という条件でAチームが1勝する確率は、Aチームの実力が0.6の確率にAチームが勝つ確率(実力)0.6を掛けた値というふうになる。続いて のときは、 これでAチームのそれぞれの事前確率のときにAが勝つ確率が求まった。で、今Aチームが勝った時、どの実力が原因で勝ったのかの確率は上の確率のままではダメ。それは、3つの場合の確率を計算すると で足しても1にならない。確率は全部の事象(おきる事柄)の確率の和は1とするので1となるよう上を調整する。 そうすると、Aが勝った(この場合1勝した)のは実力がaであったから、つまりAが勝ったという条件でAの実力が0.6, 0.5, 0.4のそれぞれについての確率を求めることができる。
それを , , こう書く。このように原因と結果を逆して書く。文章にすると「Aが勝ったという条件でAの実力が0.6, 0.5, 0.4である確率」になる。生じた結果から原因の確率を計算するのがベイズ流であるらしい。 となる。 のときは、1勝後の確率(事後確率)は事前確率のままで変化してない。のときは勝ったという結果をみて、この仮定は確からしいと思うので事後確率が大きくなり、逆にのときは、弱いはずはなかったのかと事後確率が小さくなる。このことは、現実にそぐう。ただ、確率の数値については完全に納得できたわけではなく、そんなもんなのかという感想となる。
この段階で整理すると、対戦前に理由不十分(主観)で3通りのAの実力が平等(仮定)だと言っていた人はAが1勝したという事実(結果)をもって、上のように主観確率を変えるべきだになる。ではAの実力を総合的にどう見積るかといえば、平均値(というか重心)をとるのだが確率のときは期待値という Aチームがほんの少し強いと考えを変えるべきだ。
Aチームが2勝した後
同様に、第2戦目の後どうなるか計算する。1勝後の事後確率を2戦目の事前確率として である。Aが連勝したときの確率は 上の確率の合計はだから、正規化(総和を1に)して、それぞれの事後確率を求める となる。 2連勝後はAチームの実力がという確率はより小さくなる。Aチームの実力の期待値は Aチームの方がちょっと強いと見積るべきとなる。Aチームが3勝した後
続いて、第3戦目の後どうなるか計算する。3戦目の前の事前確率は である。Aが3連勝したときの確率は 上の確率の合計0.526で正規化すると 3連勝後はAチームの実力がという確率、つまりAチームの方が強いという確率は、5割を超える。 Aチームの実力は このように見積るべきとなる。2連勝後と3連勝後のAチームの強さの見積はあまり変わらない。#####################
Aチームが4勝した後
最後に、第4戦目の後、Aチームが4連勝で日本シリーズを制したとき、Aチームの強さをどのように見積るべきかを計算する。4戦目の前の事前確率は である。Aが4連勝したときの確率は 上の確率の合計0.5376で正規化すると ところで、これら値は前回計算した4連勝決着確率(https://ykdn.blog.so-net.ne.jp/2019-07-28#wariai)と同じ数値になっている。ベイズの定理といっても素人が普通に考えても同じ数値になるのだから難しくはないのだろう。ただ、持って回った言い方をしているので混乱するのではなかろうか。4連勝後の期待値は、Aチームの実力は このように見積るべきとなる。4連勝後のAチームの強さの見積は、こんなものだ。それは、仮定が3通りだったから。Aチームが強くても と仮定しているのだ当たり前の数値だ。
Aチームの実力を0~1の連続した値で計算したらどうなるのだろうか。
日本シリーズ4連勝(03) [確率統計]
Aチームが4連勝したのは何故か?
前回実力差があるときの4連勝決着確率(9パターン)の表を示したが、たとえば今ここにAチームの4連勝決着例が示されたときAチームの実力を0.1~0.9として対戦前のAチームの実力をどのように見積ればいいのだろうか。Aが勝つ確率が0.1のときは4連勝する確率が0.0001で1万分の1だからそれはありそうにもない。Aが勝つ確率が0.9のときは4連勝する確率が0.6561で十分にありそうだ。でもAが勝つ確率が0.9ということ自体ありそうな仮定なのか?極端に言えばAが勝つ確率が1のときは4連勝する確率が1でこれ以外にない。でもAが勝つ確率が1ということはあまりに乱暴な仮定ではないか。3パターンで考える4連勝決着確率
4連勝決着確率(9パターン)では複雑になるので、AチームとBチームの実力を仮に次の3通りのいずれかでどれが一番確からしいかとかは分からず、皆平等だと考える。Aチームの勝つ確率を の3通りでそれらの確率は
と考える。この予め仮定したの確率のことを事前確率というようだ。
Aチームが強いと考えれば、 のとき事前確率を大きめに、他の確率を小さめにして合計確率を1とする。逆もまたしかり。
3パターンそれぞれでAの4連勝で決着する確率を計算してみる。 のとき(という条件で)Aが4連勝する確率はである。条件付確率というそうだ。これを数式で下のように表す。 同様に は 当然Aチームの方が強ければ4連勝となる確率も高くなるのだが、その確率は他の場合と比べてどの位なのかを調べたい。4連勝となる確率の比を取ってみる。 Aチームが強いとき は五分五分のときと比べ4連勝する確率は倍大きくなる。だからどうしたということになるのだけれども、2倍くらいじゃ、絶対Aチームの方が強いとは言えず、多分Aチームの方が強いのじゃないだろうかなぁ?多分ネッ?てなもんだ。この割り算したときの比のことを尤度比というのかと思ったけれどそうではない。単に確率の比をとっただけ。
もうちょい計算してみる。
割合を調べてみる。
で、この値は何だ?3通りの実力仮定ではのときの確率がとなるということか?何か変だ。素人は無駄なことばかりしているような気がする。もっと考えてみる。



