日本シリーズ４連勝(07)

２連勝から４連勝までのＡチームの実力について事後確率分布を計算してみる

前回の復習

まず、対戦前の事前分布を一様分布としたときの確率分布関数や各統計量は前回計算したとおり
$y$ 　……　確率密度
$x$ 　……　Ａチームの実力（勝つ確率）
$y=1(0\leqq x\leqq 1)$ 　……　事前分布
$E=0.5$ 　……　期待値
$m=0.5$ 　……　確率を二等分する$x$の値。自己流。中央値に相当するか？
$OR=1$ 　……　Ａチームが強い確率が弱い確率の何倍か。自己流。オッズ比に相当するか？

続いて、１勝後の事後確率分布関数や各統計量は前回計算したとおり
$y=x(0\leqq x\leqq 1)$　……　事後分布
上を正規化（１勝した確率の合計を１に調整する）すると
$y=2x(0\leqq x\leqq 1)$　……　正規化後の分布
$E=\frac{2}{3}$ 　……　期待値
$m \fallingdotseq 0.7071$ 　……　確率を二等分する$x$の値。自己流。中央値に相当するか？
$OR=3$ 　……　Ａチームが強い確率が弱い確率の何倍か。自己流。オッズ比に相当するか？

２連勝後の事後分布(1)

初期状態の事前分布は
$$y=1(0\leqq x\leqq 1)$$ Ａチームが２連勝する確率は $x^2$ だから $$y=x^2(0\leqq x\leqq 1)$$ これが２連勝後のグラフとなる。事前分布とこれを重ねると

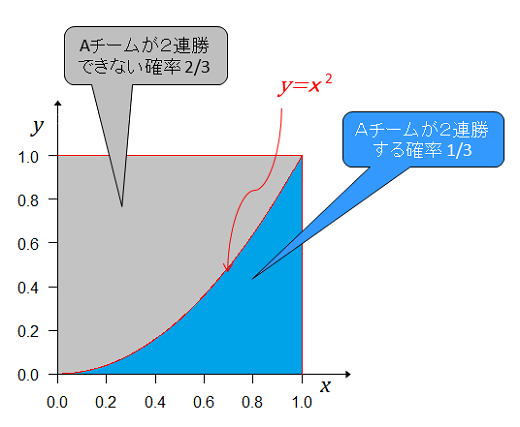
青の部分の面積は $${\int }_0^1{x}^{2}dx={\left[\frac{1}{3}{x}^3\right]}_0^1=\frac{1}{3}$$ 正規化すると（青の部分の面積を１にする。すなわち、全事象の確率（２連勝の確率の合計）を１にする。） $$y=3x^2(0\leqq x\leqq 1)$$ これが、事後分布となる。

２連勝後の事後分布(2)

これをベータ分布で考えると、ベータ分布の一般式は下記のとおりで $$y=C{x}^{\alpha -1}{(1-x)}^{\beta -1}(0\leqq x\leqq 1)$$ ここで、
$y$ 　……　右辺での確率密度
$C$ 　……　全事象確率を１にするための調整定数
$x$ 　……　Ａチームの実力（勝つ確率）
$1-x$ 　……　Ａチームが負ける確率
$\alpha -1$ 　……　Ａチームの勝利数
$\beta -1$ 　……　Ａチームの敗北数
２勝０敗だから $C=1,\alpha =3,\beta =1$ としてやる。
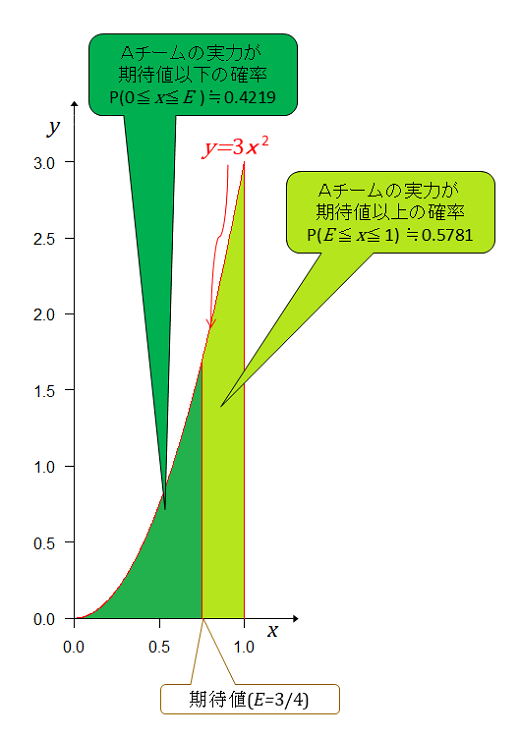
$$y=1\times x^{3-1}{(1-x)}^{1-1}=x^2$$ 前記と同様に全事象の確率が１となるようにすると事後分布は $$y=3x^2(0\leqq x\leqq 1)$$ ベータ分布の期待値$E$は $$E=\frac{\alpha }{\alpha +\beta }=\frac{3}{3+1}=\frac{3}{4}$$ である。
期待値以下の面積（確率）は $${\int }_0^{\frac{3}{4}}3x^{2}dx={\left[x^3\right]}_0^{\frac{3}{4}}={\left(\frac{3}{4}\right)}^3\fallingdotseq 0.4219$$ 期待値以上の面積（確率）は $${\int }_{\frac{3}{4}}^{1}3x^{2}dx={\left[x^3\right]}_{\frac{3}{4}}^1=1-{\left(\frac{3}{4}\right)}^3\fallingdotseq 0.5781$$ Ａチームの実力（勝率）が期待値以上である確率は期待値以下の確率の1.37倍大きい。

左右の確率が等しくなる点$m$は $${\int }_0^{m}3x^{2}dx={\left[x^3\right]}_0^m=m^3=\frac{1}{2}$$ $$m=\sqrt[3]{\frac{1}{2}}\fallingdotseq 0.7937$$
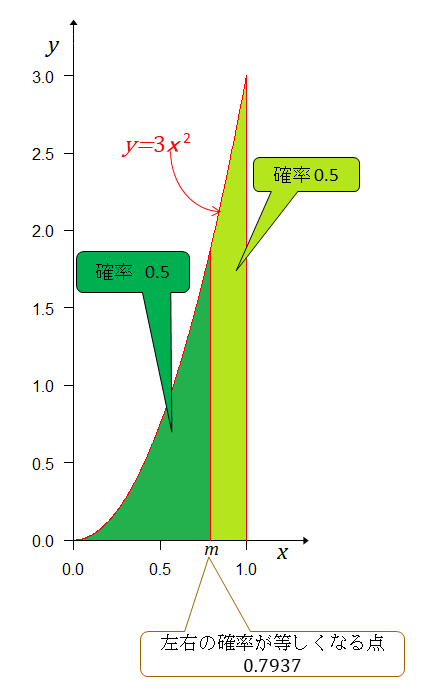
次にＡチームの実力（勝率）がＢチームより強いか、弱いかを確率で示す。 $x=0.5$が五分五分だから左（弱い）右（強い）に分けて確率を求める。 $${\int }_0^{\frac{1}{2}}3x^{2}dx={\left[x^3\right]}_0^{\frac{1}{2}}={\left(\frac{1}{2}\right)}^3=\frac{1}{8}$$ だから $${\int }_{\frac{1}{2}}^{0}3x^{2}dx=\frac{7}{8}$$ その結果が下図。

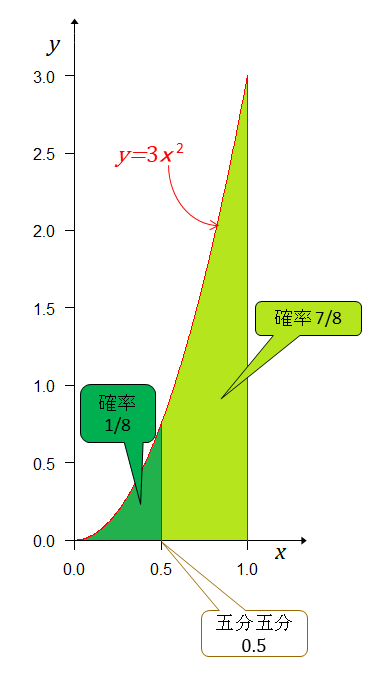
２連勝した時点でＡチームの方が強い確率が弱い確率よりも7倍も大きくなる。ベイズの定理を使って事後確率分布を計算していると自分では思っているのだが、それが正しいと考えれば、オッズ比（？）は７倍だから３戦目はＡチームが負ける方に１万円賭け、Ａチームが負けると８万円戻るという賭けとＡチームが勝つ方に７万円賭け、Ａチームが勝つと８万円戻るという賭けが平等ということになる。素人考えでは、負ける方に賭けるのが有利に感じる。

３連勝した

初期状態の事前分布は
$$y=1(0\leqq x\leqq 1)$$ Ａチームが３連勝する確率は $x^3$ だから $$y=x^3(0\leqq x\leqq 1)$$ これが３連勝後のグラフとなる。事前分布とこれを重ねると

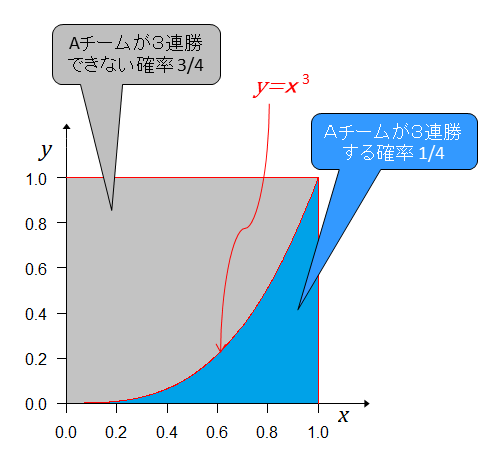
青の部分の面積は $${\int }_0^1{x}^{3}dx={\left[\frac{1}{4}{x}^4\right]}_0^1=\frac{1}{4}$$ 正規化すると（青の部分の面積を１にする。すなわち、全事象の確率を１にする。） $$y=4x^3(0\leqq x\leqq 1)$$ これが、事後分布となる。

３連勝後の事後分布(2)

これをベータ分布で考えると、 ３勝０敗だから $C=1,\alpha =4,\beta =1$ としてやる。
$$y=1\times x^{4-1}{(1-x)}^{1-1}=x^3$$ 前記と同様に全事象の確率が１となるように正規化すると事後分布は $$y=4x^3(0\leqq x\leqq 1)$$ となり、ベータ分布の期待値$E$は $$E=\frac{4}{4+1}=\frac{4}{5}$$ である。
期待値以下の面積（確率）は $${\int }_0^{\frac{4}{5}}4x^{3}dx={\left[x^4\right]}_0^{\frac{4}{5}}={\left(\frac{4}{5}\right)}^4\fallingdotseq 0.4096$$ 期待値以上の面積（確率）は $${\int }_{\frac{4}{5}}^{1}4x^{3}dx\fallingdotseq 1-0.4096=0.5904$$ Ａチームの実力（勝率）が期待値以上である確率は期待値以下の確率の1.44倍大きいが、２連勝と３連勝では大して変わらない。

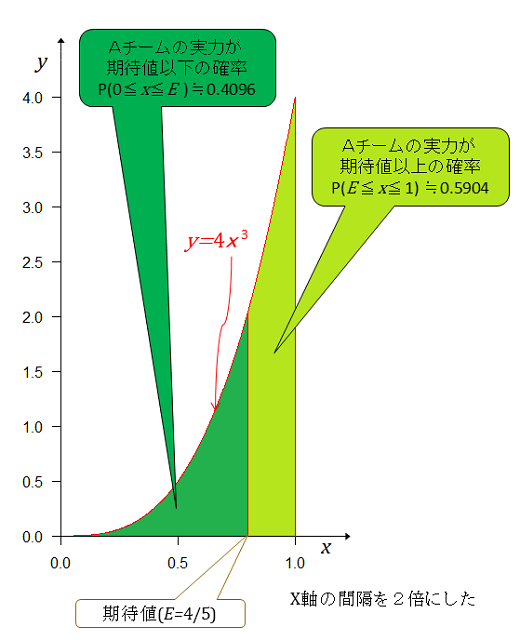
左右の確率が等しくなる点$m$は $${\int }_0^{m}4x^{3}dx={\left[x^4\right]}_0^m=m^4=\frac{1}{2}$$ $$m=\sqrt[4]{\frac{1}{2}}\fallingdotseq 0.8409$$
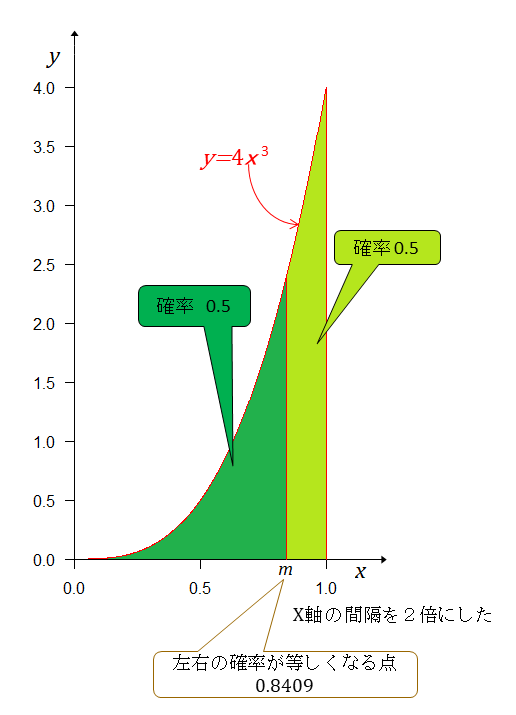
Ａチームの実力（勝率）がＢチームより強いか、弱いかを確率で示す。 $x=0.5$の左（弱い）右（強い）に分けて確率を求める。 $${\int }_0^{\frac{1}{2}}4x^{3}dx={\left[x^4\right]}_0^{\frac{1}{2}}={\left(\frac{1}{2}\right)}^4=\frac{1}{16}$$ だから $${\int }_{\frac{1}{2}}^{0}4x^{3}dx=\frac{15}{16}$$ その結果が下図。

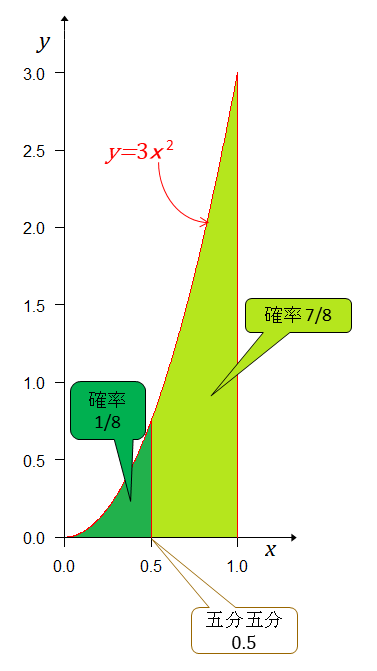
４連勝した

初期状態の事前分布は
$$y=1(0\leqq x\leqq 1)$$ Ａチームが４連勝する確率は $x^4$ だから $$y=x^4(0\leqq x\leqq 1)$$ これが４連勝後のグラフとなる。事前分布とこれを重ねると

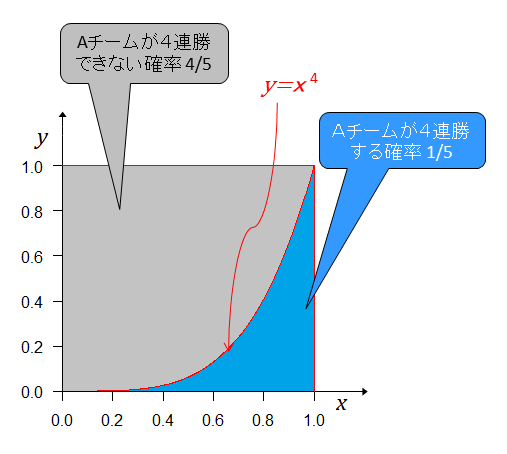
青の部分の面積は $${\int }_0^1{x}^{4}dx={\left[\frac{1}{5}{x}^5\right]}_0^1=\frac{1}{5}$$ 正規化すると（青の部分の面積を１にする。すなわち、全事象の確率を１にする。） $$y=5x^4(0\leqq x\leqq 1)$$ これが、事後分布となる。

４連勝後の事後分布(2)

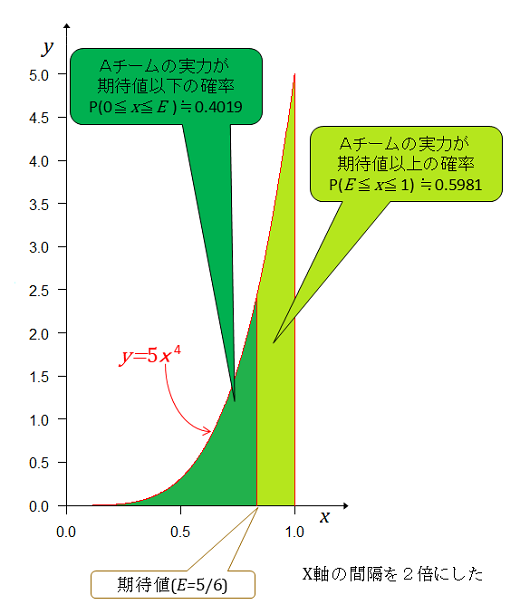
これをベータ分布で考えると、 ４勝０敗だから $C=1,\alpha =5,\beta =1$ としてやる。 $$y=1\times x^{5-1}{(1-x)}^{1-1}=x^4$$ 前記と同様に全事象の確率が１となるように正規化すると事後分布は $$y=5x^4(0\leqq x\leqq 1)$$ となり、ベータ分布の期待値$E$は $$E=\frac{5}{5+1}=\frac{5}{6}$$ である。
期待値以下の面積（確率）は $${\int }_0^{\frac{5}{6}}5x^{4}dx={\left[x^5\right]}_0^{\frac{5}{6}}={\left(\frac{5}{6}\right)}^5\fallingdotseq 0.4019$$ 期待値以上の面積（確率）は $${\int }_{\frac{5}{6}}^{1}5x^{4}dx\fallingdotseq 1-0.4019=0.5981$$ Ａチームの実力（勝率）が期待値以上である確率は期待値以下の確率の1.49倍大きいが、伸びは２連勝、３連勝、４連勝となるごとに鈍化している。

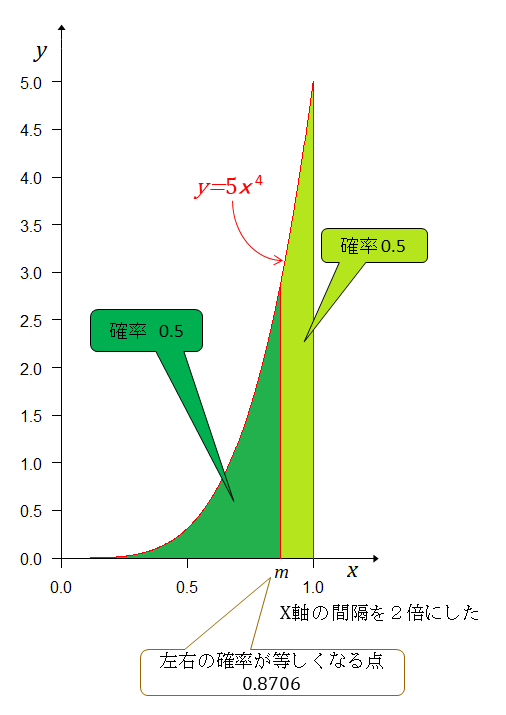
左右の確率が等しくなる点$m$は $${\int }_0^{m}5x^{4}dx={\left[x^5\right]}_0^m=m^5=\frac{1}{2}$$ $$m=\sqrt[5]{\frac{1}{2}}\fallingdotseq 0.8706$$
Ａチームの実力（勝率）がＢチームより強いか、弱いかを確率で示す。 $x=0.5$の左（弱い）右（強い）に分けて確率を求める。 $${\int }_0^{\frac{1}{2}}5x^{4}dx={\left[x^5\right]}_0^{\frac{1}{2}}={\left(\frac{1}{2}\right)}^5=\frac{1}{32}$$ だから $${\int }_{\frac{1}{2}}^{0}5x^{4}dx=\frac{31}{32}$$ その結果が下図。

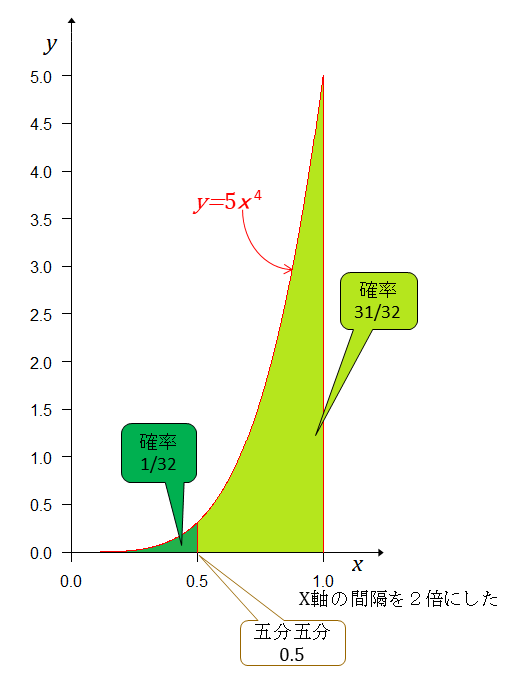
Ａチームの方が強い確率が約９７％（0.96875）だということになる。実力が互角ならどちらかが４連勝する確率は16分の2で0.125となるにもかかわらず、ベイズの定理に従って（自分ではそう思っている）計算したら、４連勝したら五分五分ではない確率が約９７％であるというわけだ。
腑に落ちない。

ベイズ推定の逐次合理性

今回は、対戦前の事前確率分布から１勝、２連勝、３連勝、４連勝後の事後確率分布を計算したが、ベイズ推定の逐次合理性というものがあって、順々に計算できるらしい。
つまり
事前分布→事後分布
として
対戦前→１勝後
１勝後→２連勝後
２連勝後→３連勝後
３連勝後→４連勝後
と事前分布を逐次更新していって計算できるとのこと。
次回、これで計算してみる。