日本シリーズ４連勝(06)

Ａチームの実力を連続変数として計算してみる

Ａチームの実力を３パターンで計算してみたが、全部を網羅して計算したい。そうすると、Ａチームの実力の期待値が計算できたり、0.5～0.6となる確率とか0.5以下のときの確率とか自由自在に計算できる。

ベイズの定理の復習と適用

まず、ベイズの定理の復習 $$P\left(A\right|B)=\frac{P\left(B\right|A\left)P\right(A)}{P\left(B\right)}$$ 各項目の意味は、
$P\left(A\right|B)$ 　……　Ｂという事象が起こったときに事象Ａが起こる確率
$P\left(B\right|A)$ 　……　Ａという事象が起こったときに事象Ｂが起こる確率
$P\left(A\right)$ 　……　Ａという事象が起こる確率
$P\left(B\right)$ 　……　Ｂという事象が起こる確率

これを今回の日本シリーズ４連勝に当てはめてみる。変数名を連想しやすく変える。
$$P\left(x\right|W)=\frac{P\left(W\right|x\left)P\right(x)}{P\left(W\right)}$$ 各項目の意味は、
$P\left(x\right|W)$ 　……　Ａチームが１勝、２連勝、３連勝もしくは４連勝したときに、Ａチームの実力が$x$である確率
$P\left(W\right|x)$ 　……　Ａチームの実力が$x$のとき、勝つ確率（それぞれの計算で１勝、２連勝、３連勝、４連勝する確率）
$P\left(x\right)$ 　……　Ａチームの実力（勝率）が$x$である確率
$P\left(W\right)$ 　……　Ａチームが勝つ確率（それぞれの計算で１勝、２連勝、３連勝、４連勝する確率）

$P\left(W\right|x)$ 　……　これを事前確率といって、事前確率（それぞれの実力$x$に対する勝つ確率）を仮定（計算）しておいて
$P\left(x\right|W)$ 　……　これを事後確率といって、対戦結果をみて真（？）の実力$x$を求める
多分、この解釈でいいと思う。

事前分布をグラフにしてみる

確率を連続変数として計算してみる。 まず、分かりやすくするため、Ａチームの実力が$x$であるときの確率密度（確率を計算するための数値で確率とは違う）を$y$として事前分布を図示する。連続変数とした段階で事前確率は事前（確率）分布、事後確率は事後（確率）分布となり期待値（平均値と言ってもいいか？）や、実力の範囲の確率（例えば実力が0.5～1とか）が計算できる。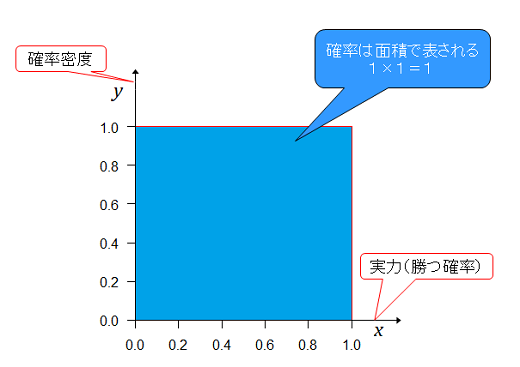

一様分布だからその式は $$y=1(0\leqq x\leqq 1)$$
このグラフ（一様分布）はベータ分布でも描けるのだが、ベータ分布の一般式は下記のとおり。 $$y=C{x}^{\alpha -1}{(1-x)}^{\beta -1}(0\leqq x\leqq 1)$$ ここで、
$y$ 　……　右辺での確率密度
$C$ 　……　全事象確率を１にするための調整定数
$x$ 　……　Ａチームの実力（勝つ確率）
$1-x$ 　……　Ａチームが負ける確率
$\alpha -1$ 　……　Ａチームの勝利数
$\beta -1$ 　……　Ａチームの敗北数
対戦前の事前分布を表すのだから、勝利数も敗北数も０にするために
$C=1$
$\alpha =1$
$\beta =1$
として $$y=1(0\leqq x\leqq 1)$$ となる。
ベータ分布にして便利な点は期待値（平均値、多分加重平均値だと思う）を簡単に計算できることがある。 ベータ分布の期待値$E$の式は $$E=\frac{\alpha }{\alpha +\beta }$$ なので、一様分布の場合は $$E=\frac{1}{1+1}=\frac{1}{2}=0.5$$ である。

１勝後の事後分布(1)

$x=0$ なら必ず負けるので $y=0$ 、 $x=1$ なら必ず勝つので $y=1$ 、 $x=0.5$ なら勝敗の確率は五分五分なので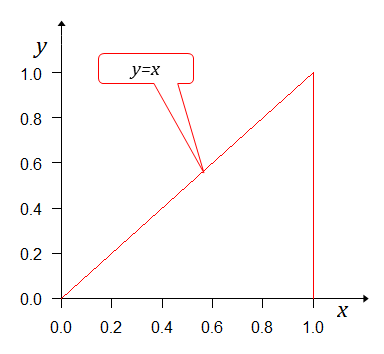 $y=0.5$ となる。つまり $$y=x(0\leqq x\leqq 1)$$
となる。

事前分布と重ねると

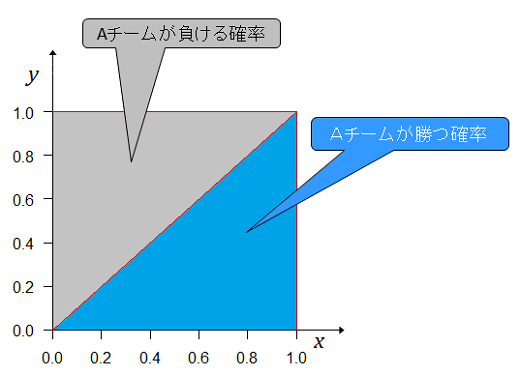
下の水色の部分がＡチームが勝った確率で上側の灰色の部分がＡチームが負けた確率になる。水色の三角形の部分の面積はＡチームの実力（勝つ確率）が０～１での第１戦目に勝つ（勝った）確率となるが、面積は底辺×高さ÷２となるので $1\times 1÷2=0.5$ である。
第２戦へは勝った方だけが行くので、勝った方の確率の合計が１となるように調整（正規化）すると下図のとおり

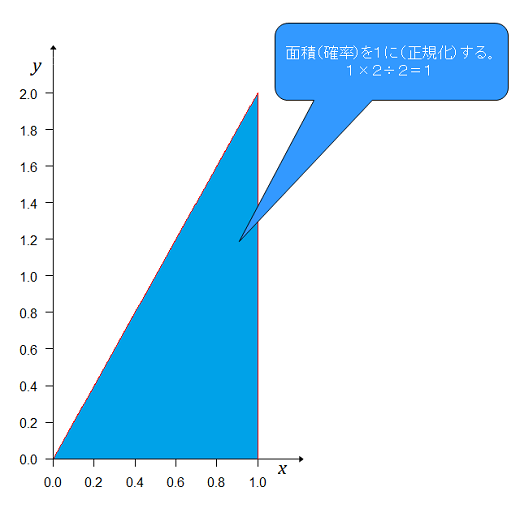
式は $$y=2x$$ これが１勝後の事後分布となる。

１勝後の事後分布(2)

念のためベータ分布でも計算してみる。１勝０敗だから $C=1,\alpha =2,\beta =1$ としてやる。
$$\begin{array}{lll}y& =& 1\times x^{\alpha -1}{(1-x)}^{\beta -1}\\ & =& x^{2-1}{(1-x)}^{1-1}\\ & =& x^1{(1-x)}^0\\ & =& x\times 1\\ & =& x\end{array}$$ 上と同様に全事象の確率が１となるようにすると $$y=2x$$ 期待値$E$は $$E=\frac{\alpha }{\alpha +\beta }=\frac{2}{2+1}=\frac{2}{3}$$ である。
１勝しただけで、Ａチームの実力（勝率）の期待値が $\frac{2}{3}$ となるが、感覚的にはたった１勝でＡチームはＢチームに対して期待値で約６割７分の勝率を見込むとは盛りすぎではないかと思うが、ベイズ流の確率計算ではこうなるのでしょうがない。ベイズ流の主観確率では対戦前の事前確率分布の期待値が五分五分と思ってたが、対戦後は事後分布の期待値が約６割７分だと思うべきだとなる。

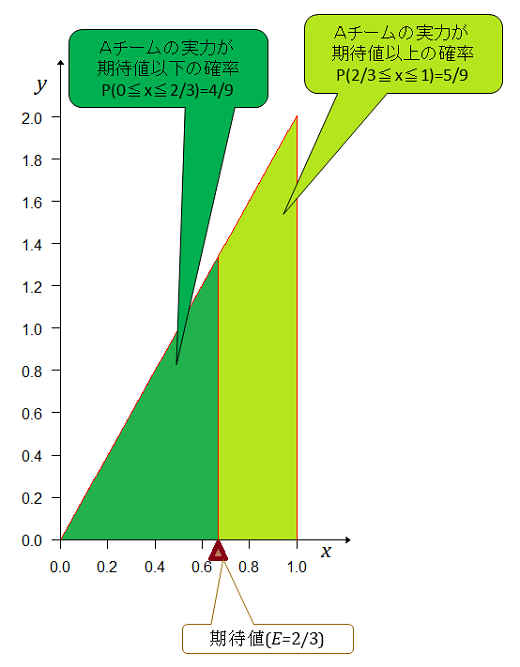
この期待値というのは、平均値ではなく加重平均（重心）であり上のように期待値を支点としてやじろべえを作ると左右が釣り合うということになる。図で見ると感覚的に釣り合うように思えない。左に傾きそう。
で、左側が期待値 $\left(E\right)$ 以下の確率 $P(0\leqq x\leqq E)$ 、右側が期待値 $\left(E\right)$ 以上の確率 $P(E\leqq x\leqq 1)$ はそれぞれ、 $$P(0\leqq x\leqq E)=\frac{2}{3}\times \frac{4}{3}\times \frac{1}{2}=\frac{4}{9}$$ $$P(E\leqq x\leqq 1)=(\frac{4}{3}+2)\times \frac{1}{3}\times \frac{1}{2}=\frac{10}{3}\times \frac{1}{3}\times \frac{1}{2}=\frac{5}{9}$$ である。Ａチームの実力（勝率）が期待値以上の確率の方が期待値以下よりも大きい（1.25倍）。こうなると期待値というのが感覚的に納得できない。
素人考えでは期待値は平均値となるべきで、図の左右の面積（確率）が等しい点、つまり確率0.5となる点ではなかろうかと。だから三角形の面積の計算で底辺×高さ÷２＝0.5。そうなる底辺を$m$とする。高さは$2m$だから。 $$m \times 2 m ÷ 2 = 0.5$$ $$m =\sqrt{0.5} \fallingdotseq 0.7071$$
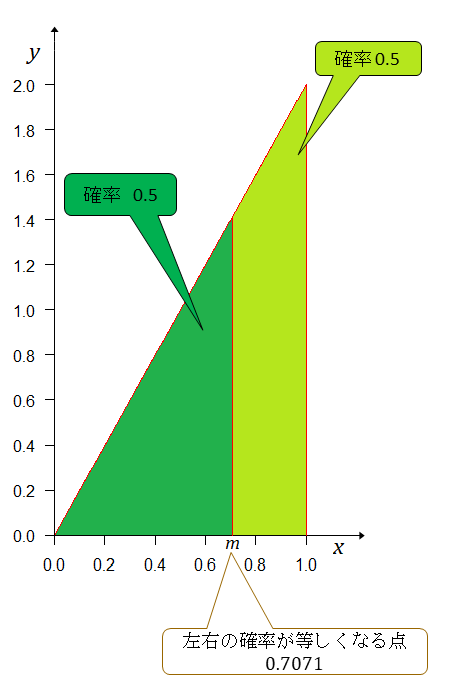
$m$は、いったい何なのだろう。平均値とは言えないのだろうな。中央値(median)かな？分からない。計算結果は、意外にも$m$の方が、期待値$E$よりもＡチームが強いと見積もられている。
別の考えをして、今度はＡチームの実力（勝率）がＢチームより強いか、弱いかを確率で示すと $x=0.5$が五分五分だから左（弱い）右（強い）に分けて確率を求める。その結果が下図。

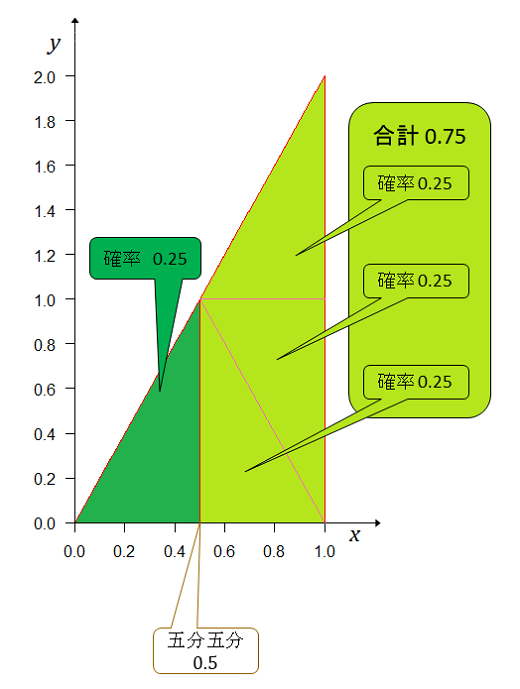
たった１勝しただけでＡチームの方が強い確率が弱い確率よりも3倍も大きくなる。たった１勝なのに。ベイズの定理を使って事後確率分布を計算していると自分では思っているのだが、この計算結果は、ちょっと感覚的になじめない。
取り敢えず、今回はここまで。次回２連勝から４連勝までの事後確率を計算する。